Wiadomości ogólne
- Czas trwania zajęć: 2 x 40 minut
- Kontekst w jakim wprowadzono doświadczenie:
Zajęcia realizowane są jako typ „zajęcia z pytaniem problemowym”. Instrukcje pojawiają się częściowo w tekście wiodącym, który ma charakter rozprawki naukowej. Proponuję przeprowadzenie doświadczenia dwuetapowo – na dwóch kolejnych jednostkach lekcyjnych. Jeśli zechcemy wykorzystać tylko 1 część, podsumowanie kończy się w punkcie 7 Zadania A.
- Określenie wiedzy i umiejętności wymaganej u uczniów przed przystąpieniem do realizacji zajęć:
Wiadomości i umiejętności dotyczące liczb pierwszych i złożonych określone w podstawie programowej dla drugiego etapu nauczania. Ponadto uczeń potrafi w podstawowym zakresie obsługiwać arkusz kalkulacyjny.
- Cele osiągnięte z wykorzystaniem doświadczenia:
Nauczyciela:
- zapoznanie uczniów ze strategiami sprawdzania, czy liczba jest pierwsza (w tym z algorytmem zwanym sitem Eratostenesa) i poszukiwania liczb pierwszych za pomocą komputera,
- wskazanie przydatności programów i narzędzi komputerowych do badań matematycznych,
- ćwiczenie analizy i krytycznej oceny tekstu matematycznego.
Uczniów:
- uczeń zna różnicę miedzy liczbami pierwszymi, złożonymi i liczbami, które nie są ani pierwsze, ani złożone,
- uczeń zna i stosuje twierdzenie o rozkładzie liczby złożonej na czynniki pierwsze,
- uczeń zna, rozumie i potrafi wykonać algorytm zwany „Sitem Eratostenesa”.
- Pojęcia kluczowe:
- liczba pierwsza,
- liczba złożona,
- dzielnik,
- podzielność liczb naturalnych.
- Potencjalne pytania badawcze:
- Jak poszukiwać liczb pierwszych?
Doświadczenie
- Zmienne występujące w doświadczeniu:
- zmienna niezależna: potencjalne dzielniki badanej liczby,
- zmienna zależna: iloraz badanej liczby przez zmienną niezależną,
- zmienna kontrolna: na każdym etapie modyfikacji algorytmu (kolejne wersje doświadczenia) stała jest zasada orzekania – jeśli otrzymamy choć jeden dzielnik naturalny, to liczba nie jest pierwsza.
Instrukcja wykonania doświadczenia:
W zależności od indywidualnej oceny nauczyciel decyduje czy poniższy program badawczy poprzedzić ćwiczeniem porządkującym rozumienie podziału liczb naturalnych na trzy podzbiory: {0, 1}, liczby pierwsze, liczby złożone. Można to np. sprawdzić proponując ocenę: która z liczb spośród: 0, 1, 2, 51 jest pierwsza i dlaczego? Uczniowie pracują w parach przez dwie minuty, a następnie na forum klasy sprawdzamy (możliwe zastosowanie metody sygnalizacji – typu światła - dla każdej z liczb) rezultat pracy i wyjaśniamy wątpliwości. Można także zapisać precyzyjną definicję liczb pierwszych, jako tych liczb naturalnych, które posiadają dokładnie dwa różne dzielniki (jedynkę i samą siebie).
Celem waszej aktywności będzie prześledzenie i zrozumienie sposobu tworzenia i modyfikacji algorytmu pozwalającego sprawdzać z wykorzystaniem arkusza kalkulacyjnego, czy dana liczba jest pierwsza. Kolejne, począwszy od drugiej, instrukcje, z wykorzystaniem których zbudujecie narzędzie badawcze, pojawiać się będą w tekście wiodącym – rozprawce traktującej o badaniach pewnego zespołu klasowego.
Zadanie A
1. Spróbujcie w parach odpowiedzieć na pytanie „Czy liczba 1361 jest pierwsza?” (to pytanie stanowić będzie wstęp do naszych badań nad algorytmizacją problemu: „Czy dana liczba jest pierwsza?”). Postawcie własną hipotezę i spróbujcie sprawdzić, pracując w parach, czy Wam się uda ją zweryfikować w ciągu dwóch minut.
(Na forum klasy należy podsumować ćwiczenie. Większości lub może nawet wszystkim parom nie uda się zweryfikować hipotezy. Ważne jest, by uczniowie opowiedzieli o swoich strategiach weryfikacji hipotezy. Na razie nie poddajemy ich ocenie. Istotnym celem tej aktywności jest bowiem nabycie doświadczenia, że proces badawczy dla dużych liczb jest pracochłonny)
Jak zauważyliście, nie jest łatwo zbadać czy liczba jest pierwsza, gdy jest ona stosunkowo duża. Dlatego współcześnie wykorzystuje się do tych badań komputery. Postaramy się także prześledzić i wykorzystać sprawozdanie z badań, których podjęła się wcześniej jedna z klas gimnazjalnych. Będziemy korzystać z fragmentów tekstu matematycznego – opisu badań nad algorytmem, który pozwala skutecznie sprawdzać czy liczby są pierwsze. Opracowanie tego algorytmu stanowić będzie klucz do rozwiązania problemu.
Za pomocą stworzonego algorytmu chcemy badać, czy są pierwsze liczby z zakresu do 10 000.
2. Wykorzystajcie pomysł Marka; wykonajcie (w zespołach 4-osobowych) w arkuszu kalkulacyjnym narzędzie do badania, czy liczba jest pierwsza wg instrukcji 1-6:
(jeśli mamy dostatecznie dużo komputerów do dyspozycji możemy pracować w parach, ale dyskusje warto prowadzić organizując zespoły 4 osobowe).
- W komórkę A2 wpisz liczbę badaną ( tu 1361).

- W komórkę A3 wpisz liczbę 2 (pierwszy potencjalny dzielnik właściwy).
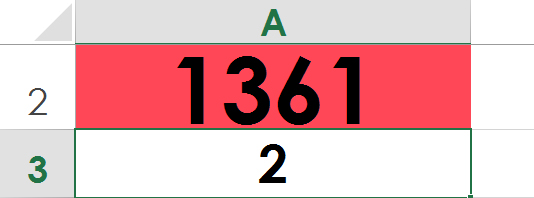
- Wypełnij wiersz trzeci serią danych o początkowej wartości 2 (A3) - krokiem 1, aż do wartości końcowej 1360.
- W komórkę A4 wpisz formułę: „=$A2/A3”, która obliczy iloraz 1361/2.
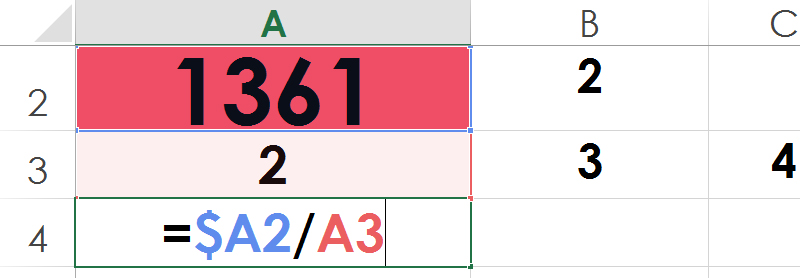
- Rozszerz formułę w wierszu czwartym, tak by otrzymać ilorazy liczby 1361 przez kolejne dzielniki naturalne z wiersza trzeciego (wykorzystaj lewy klawisz myszy)

- Sprawdź czy otrzymałeś choć jeden iloraz naturalny (wówczas liczba 1361 nie byłaby pierwsza).
- Odpowiedz na pytanie badawcze – zweryfikuj swoją hipotezę (należy sprawdzić, czy wszystkim zespołom powiodło się badanie – ewentualnie udzielić pomocy technicznej – śledząc na bieżąco jak uczniowie radzą sobie z wykonywaniem instrukcji).
3. Z którym ze stwierdzeń koleżanek i kolegów Marka się zgodzicie – przedyskutujcie to w swoich zespołach (4-osobowych):
Trudno było prowadzić obserwację dotyczącą podzielności, bo dzielników jest bardzo dużo.
Wystarczy ustawić potencjalne dzielniki do 680 (Uzasadnienie: 681 to ponad połowa liczby 1361, a przecież gdyby 1361 dzieliła się przez 681, to dzieliła by się – wcześniej, także przez iloraz tego dzielenia, czyli przez liczbę 1361/681. Ponieważ 681 to ponad połowa 1361 więc 1361/681<2, a mniejszy od 2 dzielnik właściwy nie istnieje).
(runda podsumowująca na forum klasy – szczególnie trzeba sprawdzić , czy uczniowie zrozumieli uzasadnienie z punktu b).
4. Zapoznajcie się z uwagami Joli.
Jola stwierdziła, że arkusz można jeszcze uprościć, powołując się na następujące rozumowanie: gdyby istniały liczby, przez które dzieli się 1361 to największą z nich można oznaczyć jako a.
Wynik dzielenia 1361:a - oznaczmy b.
1361:a = b, więc i 1361:b = a.
Liczba b może być co najwyżej równa a.
W tym przypadku byłoby: 1361:a = a,
Wniosek Joli: Wystarczy szukać potencjalnych dzielników liczby 1361 do liczby 36.
5. Przedyskutujcie w zespołach czy rozumowanie Joli jest poprawne.
(runda podsumowująca na forum klasy – sprawdzamy czy uczniowie zrozumieli rozumowanie Joli – można wykorzystać system świateł i nie przechodzić do kolejnego etapu bez pewności, że ten został zrozumiany przez wszystkich)
6. Zapoznajcie się teraz z propozycją Anny.
Dla każdej liczby złożonej istnieje dokładnie jeden rozkład na czynniki pierwsze. Nie musimy sprawdzać podzielności przez liczby złożone, bo badana liczba jeśli jest podzielna przez liczbę złożoną, to musi się też dzielić przez jej dzielniki pierwsze.
Wniosek Anny: Wystarczy więc, byśmy wybrali do badania liczby pierwsze mniejsze od 36 – jako potencjalne dzielniki.
7. Czy argumentacja Anny jest słuszna – przedyskutujcie to w swych grupach.
(runda podsumowująca na forum klasy – sprawdzić czy wszyscy rozumieją argumentację.W trakcie podsumowania należy doprowadzić do konkluzji, że aby zbadać, czy liczba x jest pierwsza, wystarczy zbadać czy dzieli się przez dzielniki pierwsze nie większe od √x. Zapowiadamy, że dalszą część badań warto rozpocząć od modyfikacji – uproszczenia algorytmu).
Zadanie B
Udało nam się zoptymalizować algorytm, za pomocą którego da się badać, czy liczby są pierwsze. Kolejnym naszym celem jest zbudowanie docelowego narzędzia komputerowego (zmodyfikowanie arkusza kalkulacyjnego, którego pierwotną ideę przedstawił Marek). Chcemy z jego pomocą badać liczby nie przekraczające 10 000 w celu określenia czy są pierwsze. Wykonywać będziecie zatem kolejne etapy instrukcji naszego doświadczenia.
8. Z jakiego zakresu należy wybrać liczby pierwsze, by gwarantowały takie badanie we wskazanym zakresie? Zastanówcie się indywidualnie, a następnie skonfrontujcie swoje ustalenie z uczestnikami własnej grupy.
(na forum klasy należy ustalić, że muszą to być liczby pierwsze z pierwszej setki, bo √10000=100)
9. Do poszukiwania liczb pierwszych w pierwszej setce liczb naturalnych wykorzystacie algorytm zwany „Sitem Eratostenesa”. Wykonajcie kolejne kroki doświadczenia (algorytm Eratostenesa).
- W poniższej tabeli znajdują się liczby od 1 do 100. Wykreśl jedynkę, bo nie posiada dwóch różnych dzielników naturalnych, czyli nie może być pierwsza.
- Pierwszą liczbą pierwszą jest oczywiście dwójka i ją zostawiamy, natomiast wykreślamy wszystkie jej wielokrotności, bo dzieliłyby się nie tylko przez jeden i samą siebie, ale również przez 2.
- Zostawiamy kolejną najmniejszą, nie skreśloną liczbę, a następnie wykreślmy wszystkie jej wielokrotności - z tych samych powodów jakie wskazano dla liczby 2.
- Powyższą instrukcję powtarzamy aż do wyczerpania liczb.
(wynotowujemy na tablicy liczby, które pozostały na Sicie – zbiór dzielników pierwszych z pierwszej setki liczb naturalnych).
10. Zmodyfikujemy teraz nasz arkusz. W wiersz B wpisujemy tylko dzielniki, które pozostały „na Sicie” – nie skreślone liczby z tabeli. Pozostałe komórki w wierszu B i odpowiadające im – w wierszu C - czyścimy.
11. Testujemy działanie arkusza spisując swoje uwagi.
(na forum omawiamy uwagi grupy z testowania arkusza – przedyskutować należy co najmniej spostrzeżenie nadmiarowości potencjalnych dzielników dla mniejszych liczb)
- Podsumowania doświadczenia:
W Zadaniu A i Zadaniu B przedstawiono propozycje podsumowań kolejnych etapów badań.
Układają się one w sekwencje:
mój pogląd/pogląd wypracowany w parach- dyskusja w grupie czteroosobowej – przedstawienie wspólnie ustalonych racji na forum klasy - ostateczne ustalenie, poprzez dyskusję całego zespołu klasowego obowiązujące i wykorzystywane na dalszych etapach pracy doświadczalnej. Nie powinno się przechodzić do kolejnego etapu (kolejnego punktu/etapu instrukcji/doświadczenia) bez omówienia i wyjaśnienia wszelkich wątpliwości uczniów związanych z dobrym zrozumieniem - z czego wynikają poszczególne modyfikacje algorytmu.
Warto sprawdzić (jeśli będziemy dysponować czasem) jak uczniowie radzą sobie z rozkładem na czynniki pierwsze np. liczby 4620 oraz co zrobią, gdy trzeba będzie odpowiedzieć na pytanie jaka jest kolejna liczba pierwsza następująca po liczbie 1339.
Dla osób dobrze radzących sobie z arkuszem kalkulacyjnym można zaproponować (na pracę domową) przygotowanie arkusza, który nie testowałby liczb przez nadmiarowe, potencjalne dzielniki pierwsze (większe od pierwiastka z badanej liczby).
- Propozycja dokumentacji przeprowadzenia doświadczenia przez uczniów:
- Tabela – Sito Eratostenesa - po wykreśleniu liczb.
- Docelowa wersja narzędzia badawczego - arkusz kalkulacyjny wykonany przez uczniów po modyfikacji opisanej w punkcie 10 instrukcji (propozycja wykorzystania Excela lub Calca - przykład takiego arkusza – narzędzia dla nauczyciela dołączono do scenariusza).
- Zrzuty ekranowe z badań dla kilku wybranych liczb (minimum 5 liczb większych od 1000. Uwaga! Poniżej przedstawiono przykład, w którym wykorzystano zrzut z wykorzystaniem arkusza dostarczonego jako narzędzie pomocnicze dla nauczyciela – zrzuty uczniowskie nie muszą być podobne do tego wzoru organizacji arkusza ).
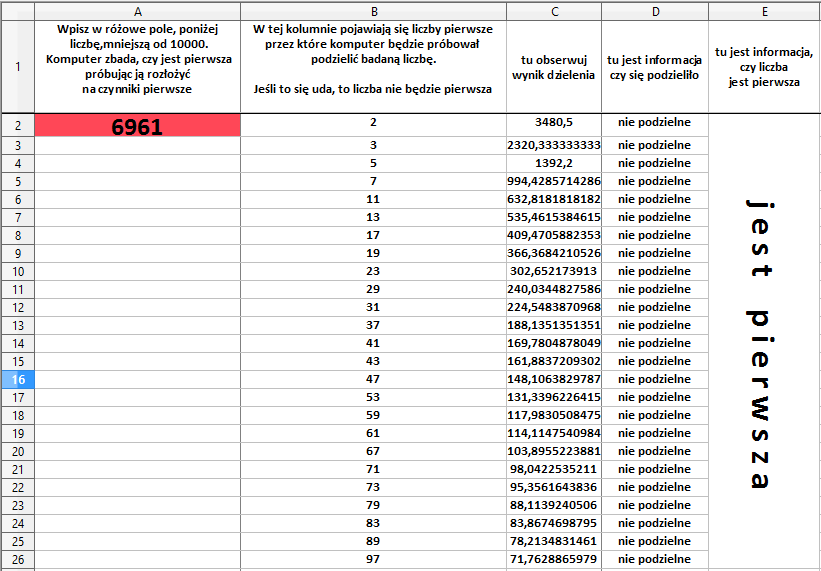
Uwaga: W materiałach do pobrania załączono gotowy arkusz kalkulacyjny "Czy pierwsza".
Podstawa programowa
- Cele, które zostaną osiągnięte w wyniku przeprowadzenia doświadczenia przez nauczyciela i uczniów pod kierunkiem nauczyciela:
a) wymagania ogólne – cele
- Drugi etap edukacyjny:
- 2 Działania na liczbach naturalnych: 8) uczeń rozpoznaje liczbę złożoną, gdy jest ona jednocyfrowa lub dwucyfrowa, a także, gdy na istnienie dzielnika wskazuje poznana cecha podzielności; 9) rozkłada liczby dwucyfrowe na czynniki pierwsze;
- Ze względu na realizację treści w gimnazjum zakres badania został poszerzony do liczb nie większych niż 10 000.
b) wymagania szczegółowe - treści nauczania
- Trzeci etap edukacyjny:
- IV Użycie i tworzenie strategii: uczeń stosuje strategię jasno wynikającą z treści zadania, tworzy strategię rozwiązania problemu.
- V Rozumowanie i argumentacja: uczeń prowadzi proste rozumowania, podaje argumenty uzasadniające poprawność rozumowania.
Materiały do pobrania
Słowniczek
EKSPERYMENT, prowadzony zgodnie z metodą naukową, rozumiany jest jako proces, w trakcie którego badacz, uczeń, wprowadza zaplanowaną zmianę jednego czynnika i bada, jakie ta zmiana przynosi rezultaty, uważając przy tym, by pozostałe czynniki pozostały niezmienne.
OBSERWACJA rozumiana jako zaplanowane gromadzenie faktów, bez wprowadzania jakichkolwiek ingerencji w badane zjawisko. W trakcie obserwacji nie występuje zmienna niezależna, ponieważ nie ingerujemy w badany proces.
Eksperyment i obserwacja są realizowane zgodnie z metodą naukową, a to oznacza:
Postawienie PYTANIA BADAWCZEGO - Pytanie może być zadane przez uczniów lub zaproponowane przez nauczyciela. Pozwala to ukierunkować myśli i skoncentrować się na badanym problemie, uświadamia, że badania naukowe są wynikiem zaplanowanego działania.Dobrze skonstruowane pytanie badawcze jest pytaniem otwartym - uczeń sam chce znaleźć na nie odpowiedź.
Kolejnym krokiem jest postawienie HIPOTEZY, czyli prawdopodobnej, przewidywanej i wymyślonej przez uczniów odpowiedź na pytanie badawcze. Pamiętajmy, że przed wykonaniem eksperymentu nie ma złych lub dobrych hipotez, każda, nawet najbardziej śmiała jest dopuszczalna.
Kolejny etap to określenie ZMIENNYCH:
- ZMIENNA NIEZALEŻNA czyli to, co zmieniamy.
- ZMIENNA ZALEŻNA czyli wielkość, którą będziemy mierzyć, obserwować.
- ZMIENNE KONTROLNE czyli wszystko to, co musi zostać niezmienne.
ZMIENNA ZALEŻNA to parametr mierzony podczas doświadczenia, zmieniający się w zależności od zmian ZMIENNEJ NIEZALEŻNEJ.
W doświadczeniu naukowym pojawiają się również PRÓBY KONTROLNE. Bez kontroli nie można jednoznacznie stwierdzić, czy wyniki doświadczenia są wiarygodne. Kontrola pozytywna to dodatkowa próba, którą przeprowadzamy identycznie, jak próbę badawczą, ale z użyciem takiego czynnika (jeśli jest znany), który na pewno wywołuje pożądany efekt. Z kolei kontrola negatywna to dodatkowa próba, ale bez użycia czynnika, o którym wiemy, że wywołuje badane zjawisko. Z założenia, wynikiem tej próby będzie brak zmiany mierzonego parametru. Nie w każdym układzie doświadczalnym da się zaplanować obie próby kontrolne.
Zajęcia z pytaniem problemowym zakładają dyskusję między uczniami na podstawie dodatkowych pytań lub przykładów dostarczonych przez nauczyciela. Zajęcia te kształcą umiejętność doboru i formułowania argumentów, słuchania osób o innym stanowisku oraz wyciągania wniosków. W wyniku dyskusji cenne byłoby wypracowanie stanowiska, by uczniowie przekonali się, że każda konstruktywna rozmowa powinna zakończyć się rzetelnym podsumowaniem.
Gry dydaktyczne wykorzystują czynnik zabawy, co wspomaga przyswajanie wiedzy przez uczniów. Gry rozwijają pomysłowość, aktywność, samodzielność, umiejętność pracy w grupie oraz uczą radzenia sobie z emocjami. Grając uczymy się przez działanie i przeżywanie. Sukcesem jest osiągnięcie celu, a nie wygrana z innymi, czy zajęcie pierwszego miejsca. Najważniejsza w grze jest dydaktyka. Wygrywać mają wszyscy.
Bibliografia
Proponuję zachęcić uczniów do poszerzenia wiedzy na temat badań związanych z poszukiwaniem liczb pierwszych za pomocą komputerów i zastosowania tych liczb np. w kryptologii. Warto nadmienić, że każdy ma możliwość wzięcia udziału w takich badaniach wykorzystując swój komputer i przekazane oprogramowanie - jeśli przystąpi do jednego z kilku prestiżowych projektów badawczych. Wystarczające informacje gimnazjaliści mogą znaleźć np. w Wikipedii:
1. http://pl.wikipedia.org/wiki/Liczba_pierwsza