Wiadomości ogólne
- Czas trwania zajęć: ok. 40 minut
- Kontekst w jakim wprowadzono doświadczenie:
Wprowadzając pytanie badawcze, można się odwołać do wcześniejszych doświadczeń uczniów np. dotyczących projekcji filmów, gdy duży obraz na ekranie jest powiększoną klatką filmową i jest podobny (w znaczeniu geometrycznym) do obrazu utrwalonego na płaskiej klatce filmowej. W proponowanym doświadczeniu nawiązano do sytuacji, z którą uczniowie mogą się zetknąć bezpośredniego – konieczności otrzymania na przenośnym ekranie prostokątnego obrazu z projektora multimedialnego. Jeśli mamy możliwość taką sytuację realnie zaaranżować – może stanowić doskonały wstęp do proponowanej obserwacji. Pamiętać należy, że model z projektorami (kinowy i multimedialny) jest tylko w przybliżeniu równoważny idei jednokładnego powiększania figur. Decyzji nauczyciela pozostawiam, czy pojęcie jednokładności zostanie konsekwentnie wprowadzone i rozwijane; w tym również zasada powstawania obrazów dla skali ujemnej (np. z wykorzystaniem zasady działania camera obscura), czy „ukrywane” – jako nie pojawiające się jawnie w podstawie programowej. Proponuję wykorzystać instrukcję zawartą w tekście przygotowanej na potrzeby tego scenariusza rozprawki, która stanowi dla uczniów oś organizującą aktywności badawcze.
- Określenie wiedzy i umiejętności wymaganej u uczniów przed przystąpieniem do realizacji zajęć:
Konieczna jest znajomość własności figur podobnych. Nie wystarcza tu, proponowane w niektórych podręcznikach, określenie (czasem niesłusznie traktowane jako definicja – choć poprawnie oddające ideę podobieństwa), że figury podobne to figury o takim samym kształcie.
- Cele osiągnięte z wykorzystaniem doświadczenia:
Nauczyciela:
- poznanie przez uczniów sposobu otrzymywania figur podobnych z wykorzystaniem jednokładności,
- odkrycie zasady konstruowania figur jednokładnych.
Uczniów: - ustalisz zmienne dla każdego z dwóch doświadczeń (Maćka i Gosi),
- będziesz wiedział jak można powiększać i pomniejszać figury zachowując ich podobieństwo,
- będziesz umiał konstruować figury podobne z wykorzystaniem poznanego sposobu.
- Pojęcia kluczowe:
- podobieństwo figur (w zależności od decyzji nauczyciela – jednokładność).
- Potencjalne pytania badawcze:
- Który ze sposobów: zaproponowany przez Maćka czy przez Gosię pozwoli uzyskać trójkąt podobny?
- Hipoteza sformułowana przez uczniów:
- H1: Pomysł Gosi jest dobry.
- H2: Pomysł Maćka jest dobry.
- H3: Rację ma Ania - żaden pomysł nie jest dobry.
Doświadczenie
- Zmienne występujące w doświadczeniu:
Dla doświadczenia Maćka:
- zmienna niezależna: odległości kadru filmowego oraz ekranu od punktowego źródła światła;
- zmienna zależna: odległości od żarówki do wierzchołka kadru i od wierzchołka kadru do wierzchołka obrazu (dla wszystkich trzech wierzchołków trójkąta);
- zmienna kontrolna: krotność powiększenia oraz podobieństwo figur.
Dla doświadczenia Gosi: - zmienna niezależna: odległości obrazu od kadru filmowego;
- zmienna zależna: obserwujemy czy figury będą podobne;
- zmienna kontrolna: odległości między wierzchołkami kadru filmowego a odpowiednimi wierzchołkami ich obrazu są takie same dla każdej z trzech par. Nie zmieniamy także odległości kadru od punktowego źródła światła.
Instrukcja wykonania doświadczenia:
Zadanie A
Gosia, Ania i Maciek mieli za zadanie przygotować urządzenia multimedialne do publicznej prezentacji w świetlicy szkolnej ich projektu geometrycznego – o konstrukcjach. Postanowili zrobić próbę projekcji swojej prezentacji wiodącej. Wypożyczyli przenośny ekran, laptop i projektor multimedialny, by pod opieką Pani ze świetlicy sprawdzić, czy podczas wystąpienia ich zespołu projektowego nie zdarzą się jakieś niespodzianki techniczne. I chyba dobrze, że zrobili próbę, bo wiele kłopotu sprawiło im takie ustawienie projektora i ekranu, by obraz rzeczywiście był prostokątny. Nazajutrz Ania zaskoczyła ich propozycją, by wyjaśnić dlaczego obraz stale próbował być czworokątem niepodobnym do prostokąta, skoro w klasie nie było z tym problemu. Gosia i Maciek obiecali, że nad tym pokombinują. Gdy spotkali się ponownie, Gosia powiedziała, że według niej
„idealny obraz – podobny do oryginalnego slajdu, otrzyma się wówczas, gdy każdy punkt na ekranie będzie o tyle samo odległy od odpowiadającego mu punktu na slajdzie”.
Maciek był jednak odmiennego zdania. Jego koncepcja była bardziej zawiła i tak ją wyjaśnił:
„obraz podobny będzie wtedy, gdy każdy punkt na ekranie zostanie oddalony od swego oryginału tyle samo razy w stosunku do odległości oryginału od źródła światła”.
Ponieważ dziewczęta nie bardzo to zdanie zrozumiały zrobił im rysunek dla dwukrotnego powiększenia:
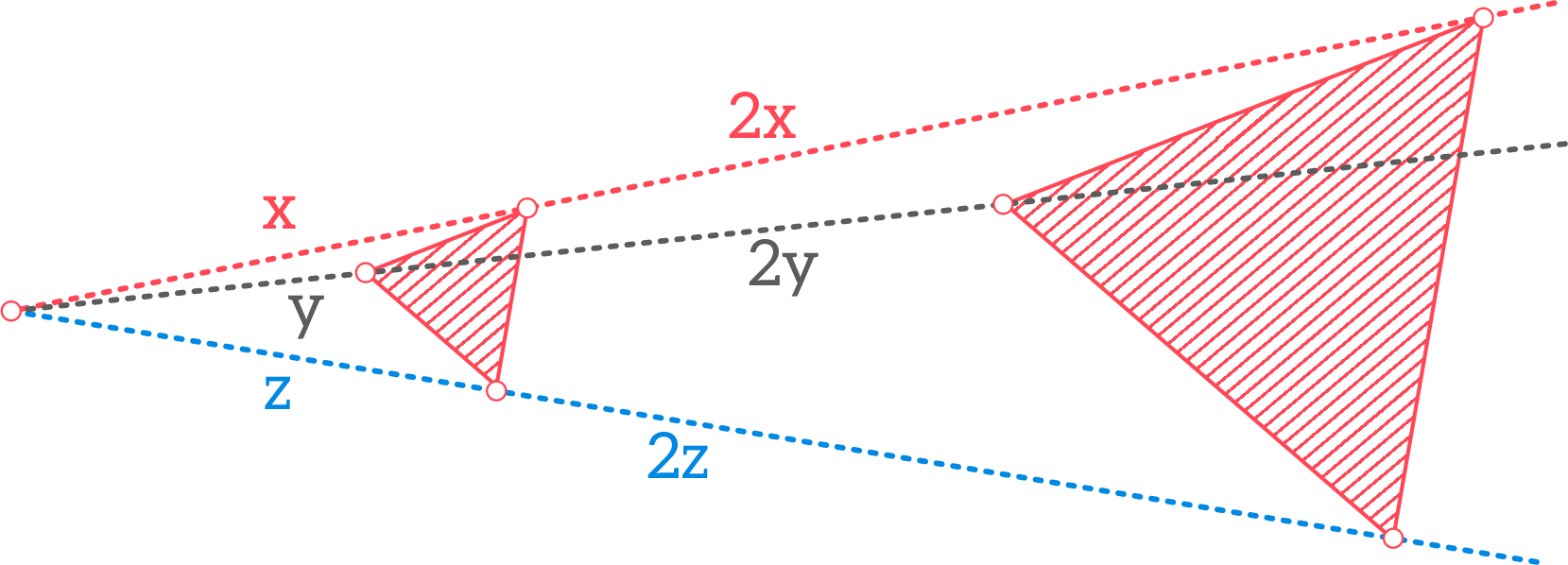
Gosia natychmiast postanowiła zilustrować rysunkiem swoją koncepcję:
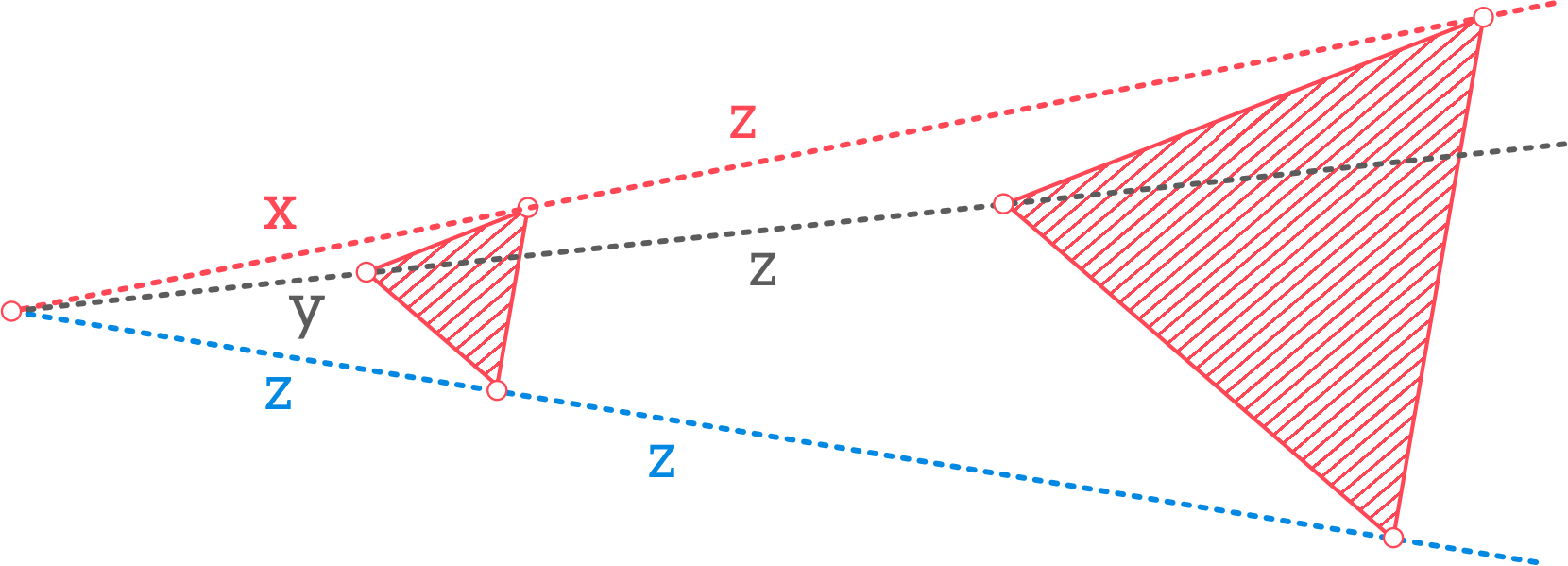
Ale czemu uparliście się na trójkąty i do tego chyba równoboczne, przecież my chcieliśmy otrzymać prostokąt? - spytała Ania.
Tu akurat Gosia i Maciek mieli podobne argumenty:
- po pierwsze istotna jest zasada, więc jeśli jest prawidłowa, sprawdzi się także dla prostokąta,
- po drugie, jak pamiętasz z geometrii, kształt wielokąta utrzymywany jest przez wzajemne położenie wierzchołków, więc czym ich mniej, tym łatwiej prowadzić analizę,
- po trzecie trójkąt jest równoboczny, bo podobieństwo musi zachowywać kąty i od razu będzie widać, czy się nie robi jakiś inny rodzaj trójkąta,
- przy okazji boki powinny być proporcjonalne, więc to także przemawia za wyborem trójkąta równobocznego – nie trzeba robić skomplikowanych pomiarów i dzieleń.
- OK, rozumiem, ale wiecie co, myślę, że żaden z waszych pomysłów się nie sprawdzi – powiedziała Ania.
A ty jak myślisz, kto ma rację? Zapisz swoją hipotezę w zeszycie.
Zadanie B
Ponieważ w trakcie realizacji projektu wszyscy troje nauczyli się dobrze pracować w programie Cabri i nawet kręcili filmy, za pomocą których wyjaśniali konstrukcje geometryczne, zdecydowali że przygotują model geometryczny dla każdego z pomysłów i udokumentują wynik badania za pomocą filmów. Pierwszy swoje filmy zdecydował się pokazać Maciek. Uznał, że musi opowiedzieć jaka była koncepcja jego badań:
„Postanowiłem zbudować model przypominający aparat kinowy. Mocną żarówką oświetlam kadr filmu (nasz trójkąt równoboczny). Oddalałem od żarówki kadr i ekran w ten sposób, by powstawał na ekranie powiększony (tyle samo razy) obraz podobny do tego - z klatki filmowej – czyli także trójkąt równoboczny. W ten sposób udało mi się pokazać to, co chciałem. Pierwsze dwa filmy ilustrują sytuację, gdy trójkąty podobne są w skali 2, kolejne dwa filmy wykonałem dla trzykrotnego powiększenia”.
Obejrzyj kolejne cztery filmy Maćka. Czy obserwacja pozwala potwierdzić słuszność jego hipotezy?
Zadanie C
Dziewczęta były zachwycone dziełem Maćka. Ania zapytała: „A może i twoją metodą Gosiu dało się osiągnąć podobieństwo?". Gosia uśmiechnęła się tajemniczo i odtworzyła swój film.
Obejrzyj film Gosi. Czy obserwacja pozwala potwierdzić słuszność jej hipotezy?
- Podsumowania doświadczenia:
Uczniowie najpierw w parach, a następnie poprzez odsłuchanie np. dwóch par na forum klasy ustalają, który sposób gwarantuje zachowanie podobieństwa i zapisują to w zeszycie lub w karcie pracy - można wykorzystać propozycję instrukcji dla par przedstawioną w Propozycji dokumentacji przeprowadzenia doświadczenia. Należy teraz sprawdzić, czy uczniowie potrafią praktycznie wykorzystać wiedzę – czyli czy dobrze wykonają 1. punkt instrukcji. Należy dokładnie przedyskutować w jaki sposób można sprawdzić, czy otrzymane trójkąty są podobne. Poprawność sprawdzają sobie uczniowie w parach - ocena koleżeńska i sygnalizują (np. system świateł), jak się to udało. Nauczyciel musi zadbać o to, by wszyscy uczniowie potrafili poprawnie wykonać polecenie 1. instrukcji.
- Narysuj trójkąt nierównoboczny i powiększ go trzykrotnie sposobem Maćka. Jak sprawdzisz, czy otrzymałeś trójkąt podobny?
Teraz robimy kolejną stopklatkę, by przedyskutować możliwość pomniejszania figur z wykorzystaniem koncepcji Maćka – można skorzystać z propozycji przedstawionej w Propozycji dokumentacji przeprowadzenia doświadczenia, czyli zapytać o konkretny sposób dla pomniejszenia w skali 2, 4… - Narysuj trójkąt i pomniejsz go dwukrotnie.
Ponownie korzystamy z oceny koleżeńskiej wg kryteriów wykorzystujących własności figur podobnych – ustalonych poprzednio. Dbamy, by udało się poprawnie wykonać 5 punkt instrukcji wszystkim uczniom.
- Propozycja dokumentacji przeprowadzenia doświadczenia przez uczniów:
Uczniowie powinni ustalić i zapisać podczas każdej obserwacji zmienne występujące w doświadczeniu. Proponuję, by w tym celu odpowiedzieli kolejno na następujące pytania:- Co postanowił w każdym ze swych dwóch doświadczeń zmieniać Maciek (zmienna niezależna)?
- Co chciał obserwować (zmienna zależna)?
- Co w każdym z dwóch doświadczeń nie zmieniało się (zmienna/zmienne kontrolne)?
- Co w swym doświadczeniu postanowiła zmieniać Gosia (zmienna niezależna)?
- Co należało obserwować (zmienna zależna)?
- Co było stałe w doświadczeniu Gosi (zmienna kontrolna)?
Ponadto uczniowie powinni zapisać wniosek dotyczący sposobu (jednokładnego) powiększania figur. Proponuję, by zapytać ich: „Jak, zgodnie z pozytywnie zweryfikowanym pomysłem Maćka postąpić, by powiększyć wielokąt 2 razy/ 3 razy/ n - razy?”. To powinno się zdarzyć przed wykonaniem 4. punktu instrukcji. Proponuję także zapytać uczniów: „Czy sposób Maćka pozwala zmniejszać figury zachowując ich podobieństwo?”. I dalej: „Co zrobić, by dwukrotnie (czterokrotnie) zmniejszyć trójkąt otrzymując podobny do niego?”. To powinno się zdarzyć przed wykonaniem 5. punktu instrukcji. Dokumentację stanowią więc konstrukcje wykonane podczas realizacji 4. i 5. punktu instrukcji.
Podstawa programowa
- Cele, które zostaną osiągnięte w wyniku przeprowadzenia doświadczenia przez nauczyciela i uczniów pod kierunkiem nauczyciela:
a) wymagania ogólne – cele
- I Wykorzystanie i tworzenie informacji: uczeń interpretuje i tworzy teksty o charakterze matematycznym, używa języka matematycznego do opisu rozumowania i uzyskanych wyników.
- III Modelowanie matematyczne: uczeń dobiera model matematyczny do prostej sytuacji, buduje model matematyczny danej sytuacji.
- V Rozumowanie i argumentacja: uczeń prowadzi proste rozumowania, podaje argumenty uzasadniające poprawność rozumowania.
b) wymagania szczegółowe - treści nauczania
- 10 Figury płaskie: 13) uczeń rozpoznaje wielokąty przystające i podobne.
Materiały do pobrania
Słowniczek
EKSPERYMENT, prowadzony zgodnie z metodą naukową, rozumiany jest jako proces, w trakcie którego badacz, uczeń, wprowadza zaplanowaną zmianę jednego czynnika i bada, jakie ta zmiana przynosi rezultaty, uważając przy tym, by pozostałe czynniki pozostały niezmienne.
OBSERWACJA rozumiana jako zaplanowane gromadzenie faktów, bez wprowadzania jakichkolwiek ingerencji w badane zjawisko. W trakcie obserwacji nie występuje zmienna niezależna, ponieważ nie ingerujemy w badany proces.
Eksperyment i obserwacja są realizowane zgodnie z metodą naukową, a to oznacza:
Postawienie PYTANIA BADAWCZEGO - Pytanie może być zadane przez uczniów lub zaproponowane przez nauczyciela. Pozwala to ukierunkować myśli i skoncentrować się na badanym problemie, uświadamia, że badania naukowe są wynikiem zaplanowanego działania.Dobrze skonstruowane pytanie badawcze jest pytaniem otwartym - uczeń sam chce znaleźć na nie odpowiedź.
Kolejnym krokiem jest postawienie HIPOTEZY, czyli prawdopodobnej, przewidywanej i wymyślonej przez uczniów odpowiedź na pytanie badawcze. Pamiętajmy, że przed wykonaniem eksperymentu nie ma złych lub dobrych hipotez, każda, nawet najbardziej śmiała jest dopuszczalna.
Kolejny etap to określenie ZMIENNYCH:
- ZMIENNA NIEZALEŻNA czyli to, co zmieniamy.
- ZMIENNA ZALEŻNA czyli wielkość, którą będziemy mierzyć, obserwować.
- ZMIENNE KONTROLNE czyli wszystko to, co musi zostać niezmienne.
ZMIENNA ZALEŻNA to parametr mierzony podczas doświadczenia, zmieniający się w zależności od zmian ZMIENNEJ NIEZALEŻNEJ.
W doświadczeniu naukowym pojawiają się również PRÓBY KONTROLNE. Bez kontroli nie można jednoznacznie stwierdzić, czy wyniki doświadczenia są wiarygodne. Kontrola pozytywna to dodatkowa próba, którą przeprowadzamy identycznie, jak próbę badawczą, ale z użyciem takiego czynnika (jeśli jest znany), który na pewno wywołuje pożądany efekt. Z kolei kontrola negatywna to dodatkowa próba, ale bez użycia czynnika, o którym wiemy, że wywołuje badane zjawisko. Z założenia, wynikiem tej próby będzie brak zmiany mierzonego parametru. Nie w każdym układzie doświadczalnym da się zaplanować obie próby kontrolne.
Zajęcia z pytaniem problemowym zakładają dyskusję między uczniami na podstawie dodatkowych pytań lub przykładów dostarczonych przez nauczyciela. Zajęcia te kształcą umiejętność doboru i formułowania argumentów, słuchania osób o innym stanowisku oraz wyciągania wniosków. W wyniku dyskusji cenne byłoby wypracowanie stanowiska, by uczniowie przekonali się, że każda konstruktywna rozmowa powinna zakończyć się rzetelnym podsumowaniem.
Gry dydaktyczne wykorzystują czynnik zabawy, co wspomaga przyswajanie wiedzy przez uczniów. Gry rozwijają pomysłowość, aktywność, samodzielność, umiejętność pracy w grupie oraz uczą radzenia sobie z emocjami. Grając uczymy się przez działanie i przeżywanie. Sukcesem jest osiągnięcie celu, a nie wygrana z innymi, czy zajęcie pierwszego miejsca. Najważniejsza w grze jest dydaktyka. Wygrywać mają wszyscy.
Bibliografia
Proponuję skorzystać z podręczników do matematyki w gimnazjum traktujących o podobieństwie figur np.
1. Matematyka 3. Podręcznik dla gimnazjum. Wydanie 2011. Praca zbiorowa pod redakcją M. Dobrowolskiej.
Można także korzystać z wcześniejszych wydań tego podręcznika, gdy pojęcie jednokładności nie pojawia się jako ciekawostka. To pomoże zwłaszcza uczniom pragnącym podjąć alternatywne drugie lub trzecie zadanie pracy domowej. Ponadto o zasadzie działania „camera obscura” bez trudu znajdą wiele propozycji w internecie np. w lokalizacji:
2. http://pl.wikipedia.org/wiki/Camera_obscura