Podobieństwo. Badanie własności figur oświetlonych równoległą wiązką światła

Wiadomości ogólne

• Czas trwania zajęć: ok. 40 minut
• Kontekst w jakim wprowadzono doświadczenie:
  
  Proponuję wprowadzenie ćwiczenia jako rodzaj interakcji powstających podczas realizacji instrukcji wynikających z tekstu matematycznego przedstawiającego sposób rozwiązania problemu, który zaciekawił ich rówieśnicę – Martę oraz dodatkowych instrukcji wprowadzonych przez autora. Program badawczy zakłada udział uczniów w 3 doświadczeniach: obserwacji oraz dwóch eksperymentach, przy czym drugi z nich powinien być zaplanowany i wykonany przez samych uczniów. Pierwszy eksperyment stanowi rezerwę wynikającą z naturalnych kierunków poszukiwań. W przypadku braku czasu można tej części scenariusza nie realizować.

• Określenie wiedzy i umiejętności wymaganej u uczniów przed przystąpieniem do realizacji zajęć:
  
  Uczniowie potrafią obliczyć i ewentualnie zaokrąglić stosunek długości dwóch zmierzonych przez siebie odcinków. Uczniowie wiedzą, czym w doświadczeniach są: zmienna niezależna, zmienna zależna, zmienna kontrolna.

• Cele osiągnięte z wykorzystaniem doświadczenia:
  
  Nauczyciela:
  
  • odkrycie przez uczniów własności proporcjonalności odcinków powstałych jako obraz pary w rzucie równoległym.
    
    
  Uczniów:
• zbadasz  i odkryjesz własności pary odcinków oraz ich obrazu powstającego podczas oświetlenia promieniami słonecznymi.
  
  
• Pojęcia kluczowe:
  
• podobnie jak podstawa programowa doświadczenia nie zakładają potrzeby wprowadzenia pojęcia rzutu równoległego na matematyce (ze względu na trudność uzyskania korelacji z techniką) ani konieczności odwołania się do twierdzenia Talesa. To pozostawiam decyzji samych nauczycieli. Natomiast aby osiągnąć cel propedeutyczny w zakresie kształtowania tych pojęć odwołano się do możliwości własnych doświadczeń i obserwacji uczniów, nadbudowując na nich kolejną wiedzę i umiejętności.
• uczniowie powinni jednak dobrze rozumieć co oznacza proporcjonalność odcinków i wiedzieć jak sprawdzić czy odcinki są proporcjonalne.
  
  
• Potencjalne pytania badawcze:

Przedstawiony program badań zakłada odkrywanie własności pary odcinków oświetlonych równoległą wiązką światła. W tym celu uczniowie odpowiadają (stawiając kolejne hipotezy) na następujące pytania badawcze (w tekście rozprawki sformułowano je równoważnie):

1. Czy długość obrazów ulega zmianie wraz ze zmianą kąta oświetlenia?
2. Czy ulega zmianie różnica długości odcinków przy zmianie kąta oświetlenia?
3. Czy obrazy pary odcinków są do nich proporcjonalne?

• Hipoteza sformułowana przez uczniów:

1. TAK lub NIE.
2. TAK lub NIE.
3. TAK lub NIE.

---

Doświadczenie

• Zmienne występujące w doświadczeniu:
  
  W każdym z III etapów doświadczalnych zmienną niezależną jest kąt padania promieni słonecznych. Podobnie - jako zmienną kontrolną, przyjmujemy długości odcinków podstawowych oraz sposób uzyskiwania ich obrazów (poprzez rzut równoległy). Natomiast zmiennymi zależnymi są odpowiednio:

• długości obrazów,
• różnica długości obrazów,
• stosunek długości obrazów.

Instrukcja wykonania doświadczenia:

Zadanie A

Zapoznaj się z opowiadaniem „O wędrujących ze słońcem odcinkach”.

Marta zazwyczaj podjeżdża do szkoły autobusem linii podmiejskiej (czerwony) lub PKS-em (niebieski). Odkąd pojawił się nowy podwójny przystanek Marta, oczekując na przyjazd, obserwuje jak po betonowych płytkach „wędrują wraz ze słońcem” kolorowe odcinki. Skąd się tu wzięły? Otóż brzegi wspólnego dachu wykonano z półprzezroczystych, dwukolorowych obwiedni w kolorach: dłuższy – czerwonym, zaś krótszy – niebieskim. By mogła to sobie wyobrazić jej koleżanka Ela, Marta wykonała taki rysunek:

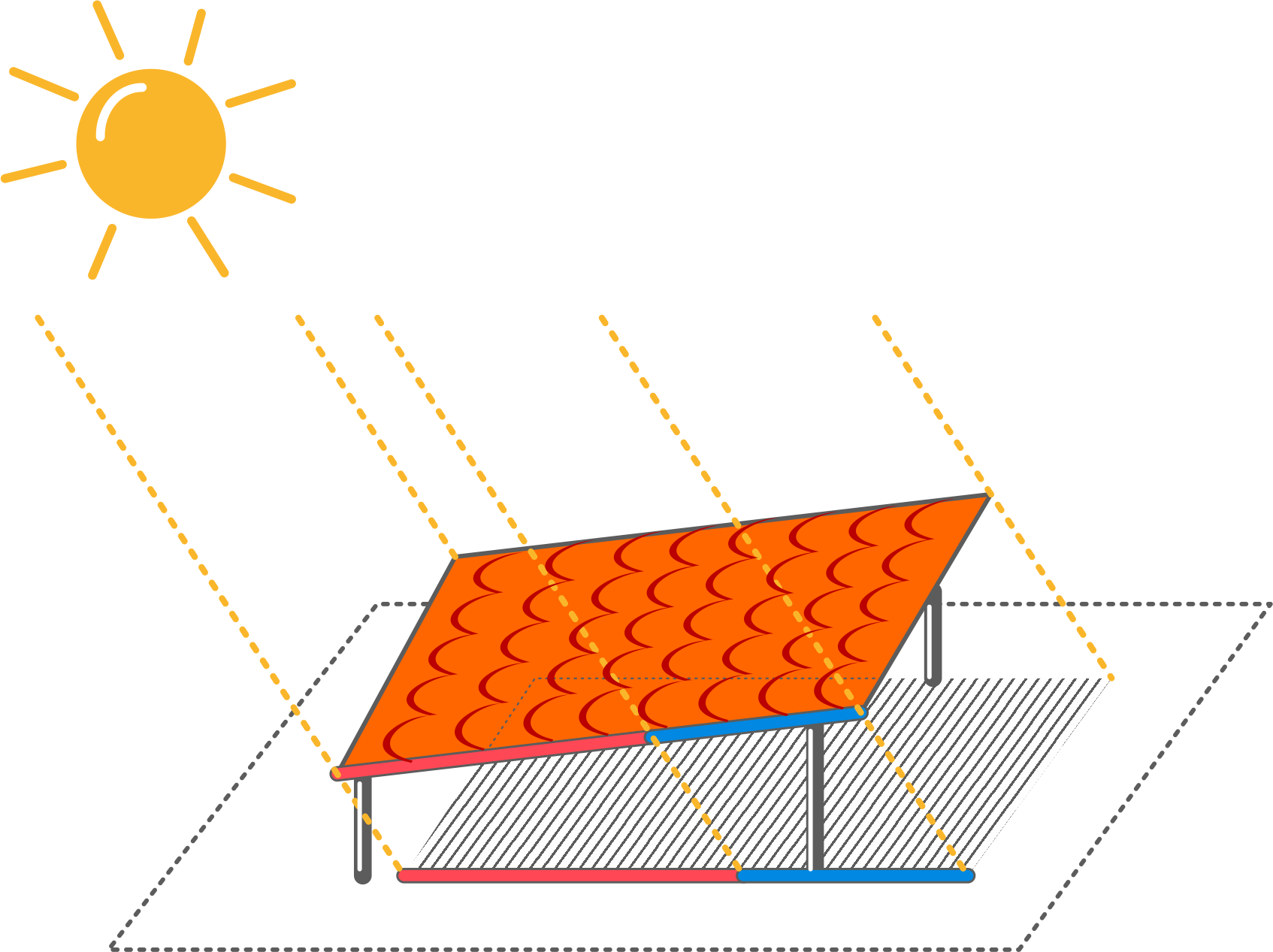
Te żółte półproste to oczywiście promyki słońca. Ponieważ Marta dojeżdża do szkoły na różne godziny, kolorowe odcinki poruszają się wraz ze słońcem. Zawsze jednak czerwony jest dłuższy, a niebieski krótszy. Martę zaciekawiło nawet, czy ich długości zmieniają się w czasie wędrówki i zaplanowała, by nazajutrz udać się na przystanek „na kilka autobusów” przed czasem, by za pomocą krawieckiej miarki przynajmniej dwukrotnie, w odstępie niemal godziny, dokonać pomiarów. Jakież spotkało ją rozczarowanie, gdy następny poranek okazał się deszczowy, bez nadziei na współpracę ze strony naszej gwiazdy dziennej. Po powrocie ze szkoły Marta nie mogła się doczekać kolejnego dnia. Ale prognozy pogody nie były optymistyczne; „zaniosło się” przynajmniej na tydzień. I wtedy doznała olśnienia. Przecież już raz narysowała dla Eli rysunek. Może dałoby się zrobić model geometryczny tej sytuacji za pomocą programu do nauki geometrii, który poznała na kółku matematyczno-informatycznym? Ważne jest tylko, by promienie wyznaczające odcinki na trotuarze były równoległe (no właśnie dlaczego one są równoległe?). Marcie udało się zbudować model, za pomocą którego dokonała obserwacji i zaspokoiła swą ciekawość.

Zadanie B

Jak myślicie: Czy „wędrujące ze słońcem” odcinki zmieniały swą długość? Postawcie swoją hipotezę, a następnie przeprowadźcie obserwację, wykorzystując nagrany przez Martę film pt. „Odcinki proporcjonalne 1”.

Po obejrzeniu własnego filmu Marta była bardzo z siebie zadowolona i niemal pewna, że wędrujące odcinki nie zmieniają swej długości.

Zadanie C

A jak wy uważacie? Przedyskutujcie to w parach, a następnie zobaczcie co uzyskała Marta, gdy postanowiła skorzystać z możliwości pomiaru długości odcinków. W efekcie jej dalszych badań powstał film „Odcinki proporcjonalne 2”.

Zadanie D

Do jakich wniosków prowadzi obserwacja tego, co pokazuje ten naukowy film Marty? Zapiszcie wnioski w zeszycie.

Zadanie E

Opiszcie teraz zmienne tak, jakbyście prowadzili rzeczywistą obserwację w słoneczny dzień.

• co jest zmienną niezależną (co zmienia nam słońce)?
• co jest zmienną zależną (jaką zmianę obserwujemy)? 
• co jest zmienną kontrolną (czego nie zmieniamy)?

Zadanie F

Przeczytajcie co na zakończenie badań powiedziała Marta:
„Dobrze, że nie poprzestałam na pierwszej obserwacji. Jednak zmysły potrafią nas zwodzić. Teraz rozumiem nawet, że wędrujące odcinki zachowywały się analogicznie jak wędrujące cienie; rankiem i wieczorem są dłuższe, a w południe krótsze. Jakżeż mogłam od razu na to nie wpaść?”
I to już koniec?… Nie! Martę znów „uwiodły” wędrujące odcinki. Co tym razem zaczęło zaprzątać jej głowę?

Zadanie G

Przeczytajcie kolejny odcinek tej opowieści.
„Wiadomo: odcinki się zmieniają, bo słońce tworzy obrazy pod coraz nowym kątem. Ale te na brzegu dachu ani drgną. Stale mają tę samą długość. Jedyne co wydaje się wspólne to fakt, że zawsze czerwony wędrujący jest dłuższy od wędrującego niebieskiego” – pomyślała Marta. Ciekawe czy zawsze o tyle samo?

Zadanie H

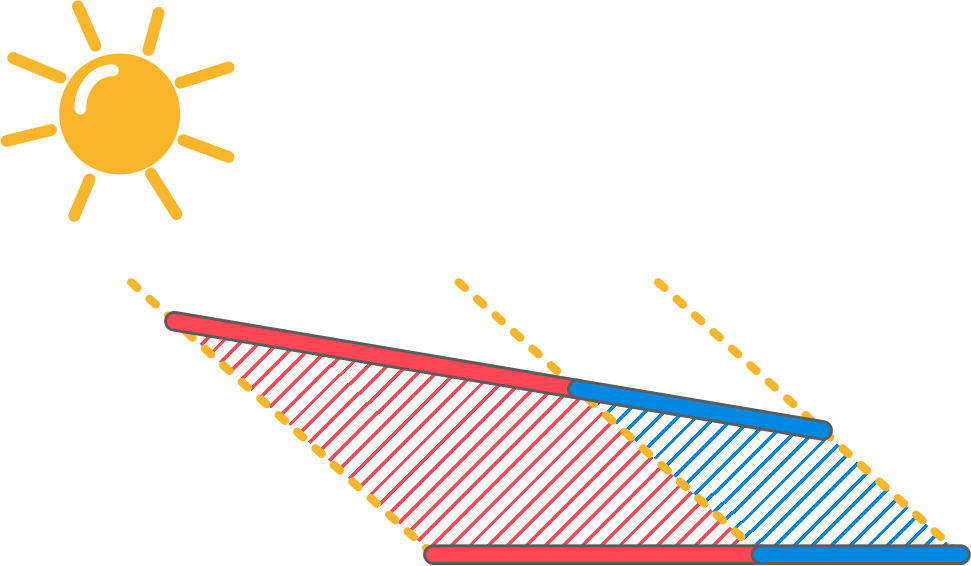
A jaką wy postawilibyście hipotezę na tak sformułowane pytanie badawcze? Ponieważ Ela (znana nam już młodsza koleżanka Marty) chciała pomóc jej w badaniach - w sposób tradycyjny, zaproponowała następujące doświadczenie:

1. Narysuję dwa odcinki; dłuższy – czerwony i krótszy – niebieski a pod nimi prostą na której pojawią się obrazy słoneczne tych odcinków (analogicznie jak na filmach Marty).
2. Przepuszczę przez końce odcinków równoległe promienie słoneczne i zaznaczę na prostej obrazy, które powstają.
3. Zmierzę długości tych obrazów i obliczę różnicę.
4. Badanie powtórzę trzykrotnie dla różnych kątów padania promieni słonecznych.

Zadanie I

Ela przesłała swoje rysunki, możecie więc sami przeprowadzić eksperyment z ich wykorzystaniem według załączonej powyżej instrukcji.

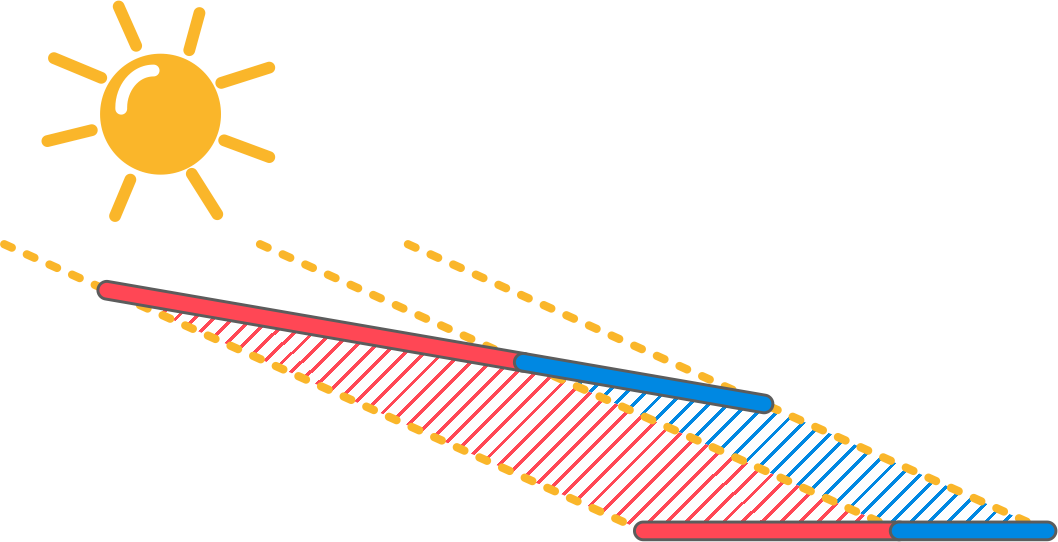
Zadanie J

Przedstawcie wnioski z waszych pomiarów.

Zadanie K

Wykorzystaj te same rysunki do odpowiedzi na jeszcze jedno pytanie, które postawiła Marta:

A może wędrujące odcinki są proporcjonalne do oryginałów, tzn. podobnie jak te z dachu przystanku pozostają do siebie w tym samym stosunku?

Postawcie własną hipotezę.

1. Wymyślcie w parach instrukcję doświadczenia.
2. Skonsultujecie ją na forum klasy.
3. Przeprowadźcie badanie.
4. Sformułujcie, a następnie przedyskutujcie wnioski.

• Podsumowania doświadczenia:
  
  Zaplanowano podsumowanie badań po każdym etapie - w postaci wniosków – zapisywanych jako odpowiedzi na kolejne pytania badawcze. Na zakończenie proponuję podsumowanie całościowe:

1. Uczniowie sygnalizują systemem świateł odpowiedzi na pytania:
   
   • Czy długość obrazów ulega zmianie wraz ze zmianą kąta oświetlenia?
   • Czy ulega zmianie różnica długości odcinków przy zmianie kąta oświetlenia?
   • Czy obrazy  pary odcinków są do nich proporcjonalne?
2. Można także zapisać podstawową własność, którą mieli odkryć w formie obejmującej szczególny przypadek, jakim jest twierdzenie Talesa:
   Jeśli dwa odcinki oświetlimy równoległą wiązką światła, to na prostej powstanie obraz w postaci pary odcinków do nich proporcjonalnych.

• Propozycja dokumentacji przeprowadzenia doświadczenia przez uczniów:
  
  Uczniowie zapisują hipotezy oraz wnioski z badań w zeszycie. Ponadto dokumentują swoje pomiary i obliczenia. Mogą je wpisywać do tabeli. Poniżej propozycja możliwego wzoru tej tabeli przy realizacji 3 etapów badań.
  

  Doświadczenie 1 – obserwacja
  Czy wędrujące odcinki zmieniają długość? WNIOSEK: _____________
  
  Do tabeli wpisz pomiary i wyniki obliczeń:

Eksperymenty	Długości odcinków oryginalnych		Rysunek Eli nr 1		Rysunek Eli nr 2		Rysunek Eli nr 3
Doświadczenie 2 eksperyment Czy wędrujące odcinki różnią się o tyle samo?	czerwony	niebieski	czerwony	niebieski	czerwony	niebieski	czerwony	niebieski
	czerwony minus niebieski →
Doświadczenie 3 eksperyment Czy wędrujące odcinki sa proporcjonalne do oryginalnych?	czerwony	niebieski	czerwony	niebieski	czerwony	niebieski	czerwony	niebieski
	czerwony podzielić przez  niebieski →

---

Podstawa programowa

• Cele, które zostaną osiągnięte w wyniku przeprowadzenia doświadczenia przez nauczyciela i uczniów pod kierunkiem nauczyciela:

a) wymagania ogólne – cele

• I Wykorzystanie i tworzenie informacji: uczeń interpretuje i tworzy teksty o charakterze matematycznym, używa języka matematycznego do opisu rozumowania i uzyskanych wyników.
• III Modelowanie matematyczne: uczeń dobiera model matematyczny do prostej sytuacji, buduje model matematyczny danej sytuacji.
• V Rozumowanie i argumentacja: uczeń prowadzi proste rozumowania, podaje argumenty uzasadniające poprawność rozumowania.

b) wymagania szczegółowe - treści nauczania

• 1 Liczby wymierne dodatnie: 2) uczeń dodaje, odejmuje, mnoży i dzieli liczby wymierne zapisane w postaci ułamków zwykłych lub rozwinięć dziesiętnych skończonych zgodnie z własną strategią obliczeń (także z wykorzystaniem kalkulatora); 4) zaokrągla rozwinięcia dziesiętne liczb; 5) oblicza wartości nieskomplikowanych wyrażeń arytmetycznych zawierających ułamki zwykłe i dziesiętne; 6) szacuje wartości wyrażeń arytmetycznych; 7) stosuje obliczenia na liczbach wymiernych do rozwiązywania problemów w kontekście praktycznym;
• 7 Równania: 1) uczeń zapisuje związki między wielkościami za pomocą równania pierwszego stopnia z jedną niewiadomą, w tym związki między wielkościami wprost proporcjonalnymi i odwrotnie proporcjonalnymi;

---

Materiały do pobrania

• pdf Proporcjonalność - procedura 474 KB
• pdf Proporcjonalność - karta pracy - wersja A 487 KB
• doc Proporcjonalność - karta pracy - wersja A 750 KB
• mp4 Proporcjonalność - animacja "Odcinki proporcjonalne 1" 3 MB
• mp4 Proporcjonalność - animacja "Odcinki proporcjonalne 2" 3 MB

---

Słowniczek

EKSPERYMENT, prowadzony zgodnie z metodą naukową, rozumiany jest jako proces, w trakcie którego badacz, uczeń, wprowadza zaplanowaną zmianę jednego czynnika i bada, jakie ta zmiana przynosi rezultaty, uważając przy tym, by pozostałe czynniki pozostały niezmienne.

 

OBSERWACJA rozumiana jako zaplanowane gromadzenie faktów, bez wprowadzania jakichkolwiek ingerencji w badane zjawisko. W trakcie obserwacji nie występuje zmienna niezależna, ponieważ nie ingerujemy w badany proces.

 

Eksperyment i obserwacja są realizowane zgodnie z metodą naukową, a to oznacza:

Postawienie PYTANIA BADAWCZEGO - Pytanie może być zadane przez uczniów lub zaproponowane przez nauczyciela. Pozwala to ukierunkować myśli i skoncentrować się na badanym problemie, uświadamia, że badania naukowe są wynikiem zaplanowanego działania.Dobrze skonstruowane pytanie badawcze jest pytaniem otwartym - uczeń sam chce znaleźć na nie odpowiedź.

Kolejnym krokiem jest postawienie HIPOTEZY, czyli prawdopodobnej, przewidywanej i wymyślonej przez uczniów odpowiedź na pytanie badawcze. Pamiętajmy, że przed wykonaniem eksperymentu nie ma złych lub dobrych hipotez, każda, nawet najbardziej śmiała jest dopuszczalna.

Kolejny etap to określenie ZMIENNYCH:

• ZMIENNA NIEZALEŻNA czyli to, co zmieniamy.
• ZMIENNA ZALEŻNA czyli wielkość, którą będziemy mierzyć, obserwować.
• ZMIENNE KONTROLNE czyli wszystko to, co musi zostać niezmienne.

ZMIENNA ZALEŻNA to parametr mierzony podczas doświadczenia, zmieniający się w zależności od zmian ZMIENNEJ NIEZALEŻNEJ.

  

W doświadczeniu naukowym pojawiają się również PRÓBY KONTROLNE. Bez kontroli nie można jednoznacznie stwierdzić, czy wyniki doświadczenia są wiarygodne. Kontrola pozytywna to dodatkowa próba, którą przeprowadzamy identycznie, jak próbę badawczą, ale z użyciem takiego czynnika (jeśli jest znany), który na pewno wywołuje pożądany efekt. Z kolei kontrola negatywna to dodatkowa próba, ale bez użycia czynnika, o którym wiemy, że wywołuje badane zjawisko. Z założenia, wynikiem tej próby będzie brak zmiany mierzonego parametru. Nie w każdym układzie doświadczalnym da się zaplanować obie próby kontrolne.

  

Zajęcia z pytaniem problemowym zakładają dyskusję między uczniami na podstawie dodatkowych pytań lub przykładów dostarczonych przez nauczyciela. Zajęcia te kształcą umiejętność doboru i formułowania argumentów, słuchania osób o innym stanowisku oraz wyciągania wniosków. W wyniku dyskusji cenne byłoby wypracowanie stanowiska, by uczniowie przekonali się, że każda konstruktywna rozmowa powinna zakończyć się rzetelnym podsumowaniem.

 

Gry dydaktyczne wykorzystują czynnik zabawy, co wspomaga przyswajanie wiedzy przez uczniów. Gry rozwijają pomysłowość, aktywność, samodzielność, umiejętność pracy w grupie oraz uczą radzenia sobie z emocjami. Grając uczymy się przez działanie i przeżywanie. Sukcesem jest osiągnięcie celu, a nie wygrana z innymi, czy zajęcie pierwszego miejsca. Najważniejsza w grze jest dydaktyka. Wygrywać mają wszyscy.

---

Bibliografia

Jeśli zdecydujemy się wskazać uczniom tradycyjny sposób wprowadzania odkrytej prawidłowości tzn. za pomocą twierdzenia Talesa, to można wykorzystać np.:

1.  Matematyka 3. Podręcznik dla gimnazjum. Wydania sprzed roku 2011. Praca zbiorowa pod redakcją M. Dobrowolskiej.

---