Wiadomości ogólne
- Czas trwania zajęć: 45 minut
- Kontekst w jakim wprowadzono doświadczenie:
Pierwsza część zajęć odbywa się w terenie (boisko szkolne lub inny teren o nieutwardzonej powierzchni) za pomocą 4x4 palików i 4 sznurków o długości np. 10 m (związane końce), cztery grupy uczniów rozpinają własne czworokąty, które nie są trapezami, starając się uzyskać czworokąt o możliwie największym polu. Nauczyciel sprawdza, czy ten warunek został spełniony.
- Określenie wiedzy i umiejętności wymaganej u uczniów przed przystąpieniem do realizacji zajęć:
Uczniowie znają wzory na pola trójkąta i czworokątów, znają pojęcie skali i potrafią obliczać długości odcinków w skali, potrafią konstruować trójkąt o danych bokach. Potrafią kreślić wysokość w trójkącie z użyciem ekierki. Znają jednostki długości i jednostki pola. Potrafią wykonywać pomiary i zaokrąglać ich wyniki z podaną dokładnością.
- Cele osiągnięte z wykorzystaniem doświadczenia:
Nauczyciela:
- zapoznanie uczniów ze sposobem obliczania pól wielokątów, gdy nie można skorzystać z gotowych wzorów na ich pola (pole figury złożonej z części),
- wykorzystanie wcześniej zdobytych przez uczniów: wiedzy i umiejętności matematycznych do rozwiązywania problemów praktycznych.
Uczniów:
- uczeń pozna praktyczny sposób na określenie pola czworokąta, który nie jest trapezem i będzie mógł go wykorzystać jako metodę dla określania pól dowolnych wielokątów,
- uczeń będzie umiał uzasadnić, dlaczego nie wszystkie pomiary wykonane zostały w terenie.
- Pojęcia kluczowe:
- wysokość trójkąta,
- pole trójkąta,
- jednostki pola,
- skala,
- konstrukcja trójkąta o danych bokach,
- pole wielokąta złożonego z części.
- Potencjalne pytania badawcze:
- Której grupie, twoim zdaniem, udało się zbudować czworokąt o największym polu?
- Hipoteza sformułowana przez uczniów:
- Uczniowie na podstawie obserwacji stawiają hipotezy i wskazują, której grupie udało się zbudować czworokąt o największym polu. Możliwe jest uznanie, że największe pole osiągnęła więcej niż jedna grupa (ich czworokąty mają największe, równe sobie pola). Hipotezę zaleca się formułować indywidualnie (bez ustalania w ramach grup).
Doświadczenie
- Potrzebne materiały, przyrządy:
- 16 palików i młotek/4młotki do ich wbijania,
- około 40 m nierozciągliwego sznurka lub 4 jednakowe kawałki, które po związaniu końców pozwalają uzyskać czworokąt o obwodzie 10m (propozycja autora – możliwość modyfikacji),
- 4 taśmy miernicze o długości 5 metrów,
- przyrządy do kreśleń i pomiarów: cyrkiel, linijka, ekierka.
- Uwagi dotyczące BHP:
Należy wybrać obszar do rozpinania czworokątów, który nie zagraża spokojnej pracy uczniów. Szczególną ostrożność należy zachować przy wbijaniu palików (wybrać teren, który to umożliwia). Należy stosować zasady dotyczące organizacji wycieczek obowiązujące w szkole, jeśli opuszczamy jej teren.
- Zmienne występujące w doświadczeniu:
- zmienna niezależna: kształt czworokąta,
- zmienna zależna: pole czworokąta,
- zmienna kontrolna: obwód czworokąta.
Instrukcja wykonania doświadczenia:
Zadanie A
- Narysujcie schemat czworokąta rozpiętego w terenie wg poniższego wzoru i zmierzcie wskazane odcinki a, b, c, d, x (starajcie się oddać przybliżony kształt waszego czworokąta).
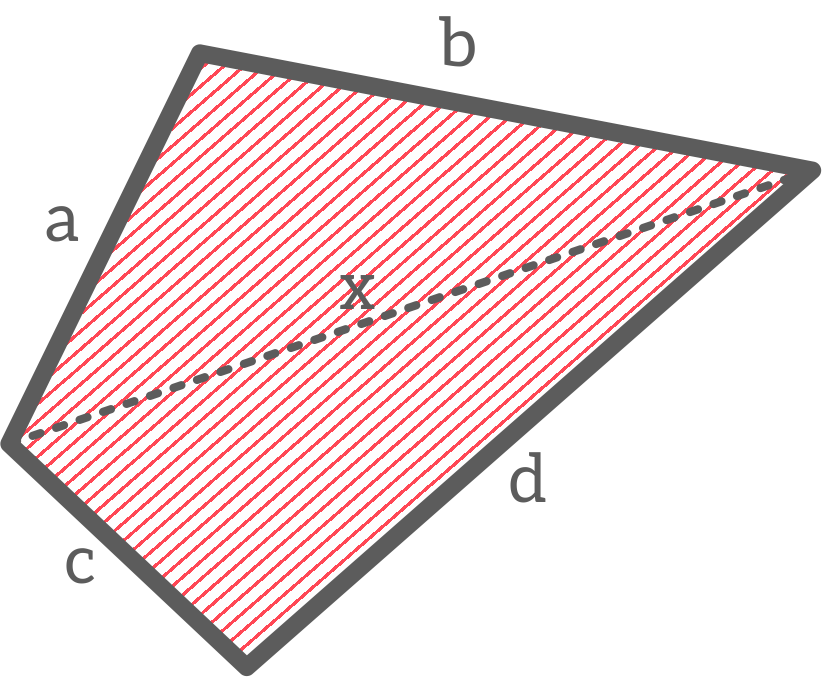
3. Obliczcie długości odcinków w skali 1:100 i wpiszcie do tabeli.
4. Narysujcie w zeszycie z dokładnością do 1 mm odcinki a’, b’, c’, d’, x’.
5. Skonstruujcie trójkąt I o bokach x’, a’, b’, a następnie „dobudujcie” konstrukcyjnie trójkąt II o bokach x’, c’, d’ tak, by powstał czworokąt o bokach a’, b’, c’, d’, będący obrazem (w skali 1:100) waszego czworokąta rozpiętego w terenie.
6. Za pomocą linijki i ekierki wykreślcie wysokości h1’ i h2’ odpowiednio w trójkątach I i II według poniższego schematu:
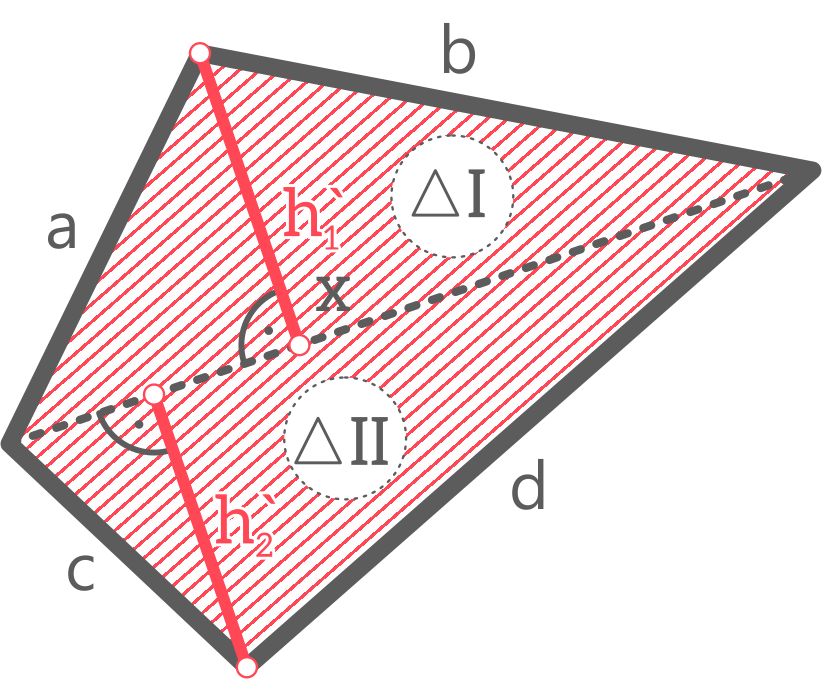
8. Obliczcie rzeczywiste wymiary wysokości tzn. h1 i h2 i wpiszcie do tabeli.
9. Obliczcie pole trójkąta o bokach a, b, x, wg wzoru P1=1/2x·h1, a następnie trójkąta o bokach c, d, x wg wzoru P2=1/2x·h2 Wyniki obliczeń wpiszcie do tabeli.
10. Obliczcie pole waszego czworokąta dodając pola trójkątów: P¸ = P1 + P2. Wynik obliczenia do tabeli.
- Podsumowania doświadczenia:
Grupy przedstawiają wyniki swoich doświadczeń (nauczyciel w trakcie pracy śledzi i sprawdza poprawność wykonywania doświadczenia, by nie otrzymali złych wyników – w razie potrzeby udziela wskazówek). Indywidualnie weryfikowane są hipotezy. Ogłaszamy, której grupie udało się zbudować największy wielokąt.
Uczniowie dyskutują w parach: dlaczego w doświadczeniu zaproponowano podział czworokątów na dwa trójkąty, a nie np. na trapez i trójkąt? Następnie przedstawiają swoje uzasadnienia i następuje krótkie podsumowanie uczniowskich wniosków na forum całej klasy. Nauczyciel dba o to, by jednym z istotnych argumentów była trudność z wyznaczaniem prostych równoległych w terenie. Następnie w innych parach należy przedyskutować, dlaczego nie mierzono wysokości trójkątów w terenie i ponownie omówić na forum klasy wypracowane wnioski.
Jako ćwiczenie utrwalające można zaproponować uczniom pracę domową polegającą na narysowaniu dowolnego pięciokąta i obliczenia jego pola przez podział na dowolne wielokąty.
Można też zachęcić uczniów (zadanie nieobowiązkowe) do zastanowienia się jak można w terenie wyznaczać odcinki wzajemnie równoległe i prostopadłe oraz nad strategią budowania czworokątów o możliwie największym polu. Jeśli któreś z zadań nieobowiązkowych zostanie wykonanych, warto omówić je na początku kolejnych zajęć (zaplanować czas).
- Propozycja dokumentacji przeprowadzenia doświadczenia przez uczniów:
Schemat czworokąta wg wzoru.
Miejsca na obliczenia pól.
P1 =
P2 =
P◊=
Tabela – do wpisywania wyników pomiarów i obliczeń.
|
a(m) |
b(m) |
c(m) |
d(m) |
x(m) |
|
|
|
|
|
|
|
a’(cm) |
b’(cm) |
c’(cm) |
d’(cm) |
x’(cm) |
|
|
|
|
|
|
|
h1’(cm) |
h2’(cm) |
h1(m) |
h2(mm) |
|
|
|
|
|
|
|
|
P1(m2) |
P2(m2) |
P∆(m2) |
||
|
|
|
|
Podstawa programowa
- Cele, które zostaną osiągnięte w wyniku przeprowadzenia doświadczenia przez nauczyciela i uczniów pod kierunkiem nauczyciela:
a) wymagania ogólne – cele
- I Wykorzystanie i tworzenie informacji: uczeń interpretuje i tworzy teksty o charakterze matematycznym, używa języka matematycznego do opisu rozumowania i uzyskanych wyników.
- II Wykorzystywanie i interpretowanie reprezentacji: uczeń używa prostych, dobrze znanych obiektów matematycznych, interpretuje pojęcia matematyczne i operuje obiektami matematycznymi.
- V Rozumowanie i argumentacja: uczeń prowadzi proste rozumowania, podaje argumenty uzasadniające poprawność rozumowania.
b) wymagania szczegółowe - treści nauczania
- 10 Figury płaskie: 9) uczeń oblicza pola i obwody trójkątów i czworokątów;
- 2 Liczby wymierne (dodatnie i niedodatnie): 3) uczeń dodaje, odejmuje, mnoży i dzieli liczby wymierne;
- z podstawy dla szkoły podstawowej – szczególnie istotne dla przedstawionego doświadczenia:
- zapisuje wyrażenia dwumianowane w postaci ułamka dziesiętnego, zaokrągla ułamki dziesiętne, mierzy długość odcinka z dokładnością do 1 milimetra, konstruuje trójkąt o trzech danych bokach, stosuje jednostki pola, oblicza rzeczywistą długość odcinka, gdy dana jest jego długość w skali, oraz długość odcinka w skali, gdy dana jest jego rzeczywista długość.
Materiały do pobrania
Słowniczek
EKSPERYMENT, prowadzony zgodnie z metodą naukową, rozumiany jest jako proces, w trakcie którego badacz, uczeń, wprowadza zaplanowaną zmianę jednego czynnika i bada, jakie ta zmiana przynosi rezultaty, uważając przy tym, by pozostałe czynniki pozostały niezmienne.
OBSERWACJA rozumiana jako zaplanowane gromadzenie faktów, bez wprowadzania jakichkolwiek ingerencji w badane zjawisko. W trakcie obserwacji nie występuje zmienna niezależna, ponieważ nie ingerujemy w badany proces.
Eksperyment i obserwacja są realizowane zgodnie z metodą naukową, a to oznacza:
Postawienie PYTANIA BADAWCZEGO - Pytanie może być zadane przez uczniów lub zaproponowane przez nauczyciela. Pozwala to ukierunkować myśli i skoncentrować się na badanym problemie, uświadamia, że badania naukowe są wynikiem zaplanowanego działania.Dobrze skonstruowane pytanie badawcze jest pytaniem otwartym - uczeń sam chce znaleźć na nie odpowiedź.
Kolejnym krokiem jest postawienie HIPOTEZY, czyli prawdopodobnej, przewidywanej i wymyślonej przez uczniów odpowiedź na pytanie badawcze. Pamiętajmy, że przed wykonaniem eksperymentu nie ma złych lub dobrych hipotez, każda, nawet najbardziej śmiała jest dopuszczalna.
Kolejny etap to określenie ZMIENNYCH:
- ZMIENNA NIEZALEŻNA czyli to, co zmieniamy.
- ZMIENNA ZALEŻNA czyli wielkość, którą będziemy mierzyć, obserwować.
- ZMIENNE KONTROLNE czyli wszystko to, co musi zostać niezmienne.
ZMIENNA ZALEŻNA to parametr mierzony podczas doświadczenia, zmieniający się w zależności od zmian ZMIENNEJ NIEZALEŻNEJ.
W doświadczeniu naukowym pojawiają się również PRÓBY KONTROLNE. Bez kontroli nie można jednoznacznie stwierdzić, czy wyniki doświadczenia są wiarygodne. Kontrola pozytywna to dodatkowa próba, którą przeprowadzamy identycznie, jak próbę badawczą, ale z użyciem takiego czynnika (jeśli jest znany), który na pewno wywołuje pożądany efekt. Z kolei kontrola negatywna to dodatkowa próba, ale bez użycia czynnika, o którym wiemy, że wywołuje badane zjawisko. Z założenia, wynikiem tej próby będzie brak zmiany mierzonego parametru. Nie w każdym układzie doświadczalnym da się zaplanować obie próby kontrolne.
Zajęcia z pytaniem problemowym zakładają dyskusję między uczniami na podstawie dodatkowych pytań lub przykładów dostarczonych przez nauczyciela. Zajęcia te kształcą umiejętność doboru i formułowania argumentów, słuchania osób o innym stanowisku oraz wyciągania wniosków. W wyniku dyskusji cenne byłoby wypracowanie stanowiska, by uczniowie przekonali się, że każda konstruktywna rozmowa powinna zakończyć się rzetelnym podsumowaniem.
Gry dydaktyczne wykorzystują czynnik zabawy, co wspomaga przyswajanie wiedzy przez uczniów. Gry rozwijają pomysłowość, aktywność, samodzielność, umiejętność pracy w grupie oraz uczą radzenia sobie z emocjami. Grając uczymy się przez działanie i przeżywanie. Sukcesem jest osiągnięcie celu, a nie wygrana z innymi, czy zajęcie pierwszego miejsca. Najważniejsza w grze jest dydaktyka. Wygrywać mają wszyscy.
Bibliografia
Pomysł doświadczenia nie został zaczerpnięty z konkretnej literatury. Uczniowie pragnąc utrwalić wiedzę lub ją uzupełnić (pomysły na wyznaczanie - nie konstrukcyjne prostopadłych i równoległych) mogą wykorzystać odpowiedni podręcznik do nauki matematyki w gimnazjum traktujący o:
- polu figury złożonej z części np. Matematyka 1. Podręcznik dla gimnazjum. Wydanie 2009. Praca zbiorowa pod redakcją M. Dobrowolskiej,
- twierdzeniu Pitagorasa np. Matematyka 2. Podręcznik dla gimnazjum. Wydanie 2010. Praca zbiorowa pod redakcją M. Dobrowolskiej,
- twierdzeniu odwrotnym do twierdzenia Talesa np. Matematyka 3. Podręcznik dla gimnazjum. Wydanie 2011. Praca zbiorowa pod redakcją M. Dobrowolskiej
Uwaga 1.: łatwiej dotrzeć do potrzebnych wiadomości wykorzystując wcześniejsze wydania, gdy twierdzenie Talesa było w podstawie programowej,
Uwaga 2.: istnieją inne niż wskazane praktyczne sposoby wyznaczania prostopadłych i równoległych w terenie - dostępne percepcji gimnazjalisty.