Podobieństwo. Praktyczne zastosowanie zależności między polami figur podobnych

Wiadomości ogólne

• Czas trwania zajęć: ok. 40 minut
• Kontekst w jakim wprowadzono doświadczenie:
  
  Jako uzasadnienie potrzeby wykonania doświadczenia wg przedstawionego planu badawczego zaproponowałem przeprowadzenie krytycznej oceny innego planu – przedstawionego we wstępie do doświadczenia. Proponuję także „niekompletny” plan badawczy (instrukcje doświadczenia), by (niektórzy) uczniowie mieli prawo popełnić ewentualny błąd powiększając pola proporcjonalnie do skali podobieństwa, a nie do jej kwadratu. Dyskusja nad rozwiązaniami powinna doprowadzić do realizacji pierwszego z celów.

• Określenie wiedzy i umiejętności wymaganej u uczniów przed przystąpieniem do realizacji zajęć:
  
  Wystarczające są umiejętności dotyczące przeliczania długości odcinków z wykorzystaniem skali oraz znajomość jednostek pola i umiejętność ich przeliczania. Uczniowie powinni także rozumieć, że działka i jej plan w pewnej skali można uznać jako figury o tym samym kształcie, czyli – podobne.

• Cele osiągnięte z wykorzystaniem doświadczenia:
  
  Nauczyciela:
  
  • odkrycie zależności dotyczącej stosunku pól figur podobnych,
  • wykorzystanie skali planu/mapy jako skali podobieństwa figur geometrycznych płaskich, do praktycznego określania pól działek.
    
    
  Uczniów:
• odkryjesz jaka jest zależność dotycząca pól figur podobnych,
• będziesz umiał określać pola działek z wykorzystaniem ich planu.
  
  
• Pojęcia kluczowe:
• podobieństwo figur,
• skala podobieństwa,
• pola figur podobnych.
  
  
• Potencjalne pytania badawcze:

1. Czy mierniczy dobrze określili pole powierzchni działki Pana Michała?

• Hipoteza sformułowana przez uczniów:

1. Prawdopodobnie uczniowie mogą stwierdzić, że mierniczy wykonali swoją pracę poprawnie lub że ich pomysł jest niepoprawny (w skrócie hipotezy brzmiałyby: TAK lub NIE).

---

Doświadczenie

• Zmienne występujące w doświadczeniu:
• zmienna niezależna: wielkość (wymiary) figur podobnych – na mapie i w rzeczywistości,
• zmienna zależna: pola figur podobnych – na mapie i w rzeczywistości,
• zmienna kontrolna: uznajemy za prawidłowy kształt określony przez geodetów.

Instrukcja wykonania doświadczenia:

Pan Michał kupił piękną płaską działkę rekreacyjną o kształcie zbliżonym do prostokąta. Na działce znajduje się altanka. Mierniczy obmierzyli brzegi działki, by obliczyć pole i ustalić jaki podatek powinien być płacony. Pan Michał, przyglądając się pomiarom zgłosił wątpliwości, czy aby poprawnie udało się wyznaczyć pole. Mierniczy przedstawili mu uzasadnienie:

Średnia długość działki: 19 m.

Średnia szerokość działki: 15 m.

Pd = 19 x 15 = 190 +95 = 285 m²

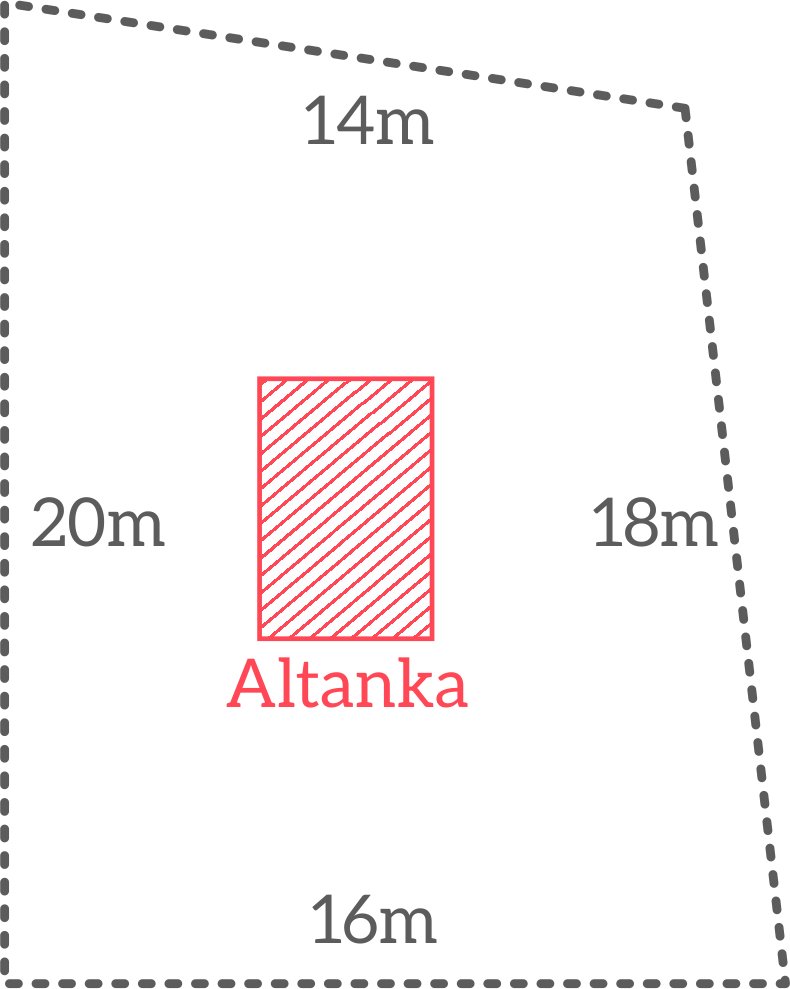
Plan działki nr 225. Właściciel: Michał Kowalski. Ul.  Drzymały 3/21; 16 - 251 Kowalewo Górne. Sporządzili w imieniu POD „Pod Dębami” mierniczy: Z. Nowak i J. Wiśniewski.

Zadanie A

Zapoznaj się z uzasadnieniem mierniczych i postaw swoją hipotezę – przewidywaną odpowiedź na pytanie badawcze:

Czy mierniczy dobrze określili pole powierzchni działki Pana Michała?

Pan Michał przekonywał mierniczych, że czworokąty o danych bokach mogą mieć różne kształty, a tym samym różne pola i zaproponował zmierzenie jeszcze przekątnej tego czworokąta, bo trójkąt o danych bokach ma kształt określony jednoznacznie. Problem polegał jednak na tym, że w wymierzeniu przekątnej przeszkadzała altanka i strony pozostały przy swych stanowiskach. Pan Michał nie dał jednak za wygraną. Postanowił skorzystać z planu działek -  dostępnym w domu działkowca. Rzeczywiście kształt jego działki wykonany przez geodetów nieco się różnił od tego, który przedstawili mu mierniczy, choć boki miały tę samą długość. Oto dokładny plan działki:

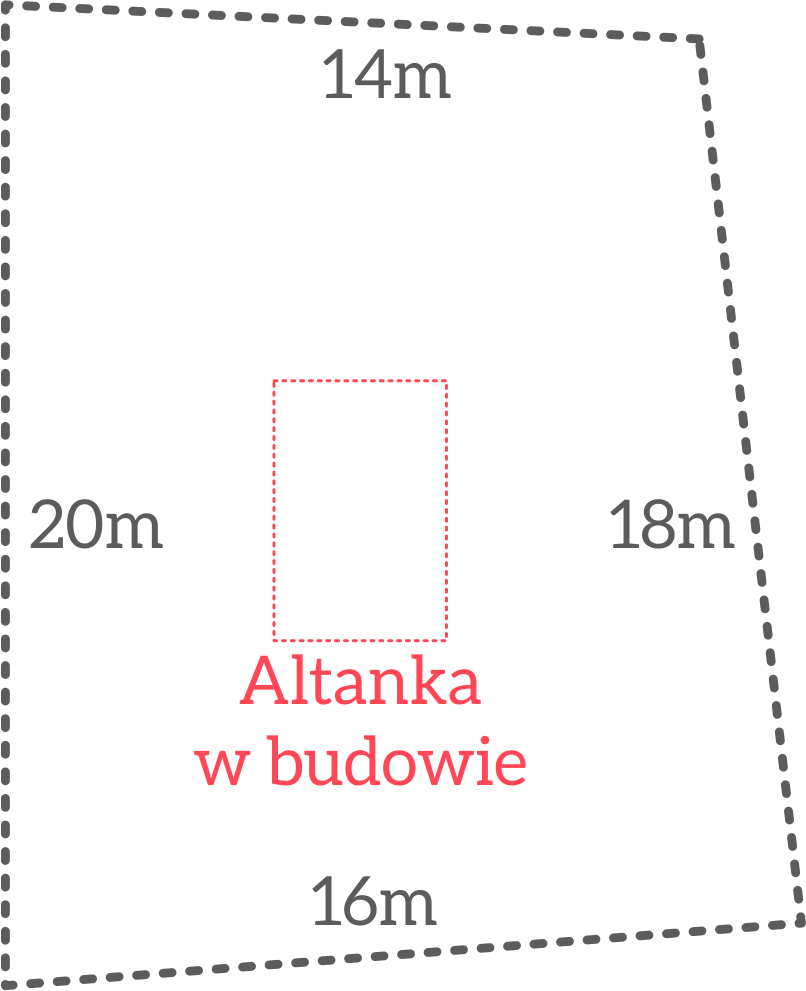
Zadanie B

W celu zweryfikowania własnej hipotezy powtórz plan badania zastosowany przez pana Michała. Oto on:

Tak postanowiłem sprawdzić czy mam rację:

1. Zmierzyć najdłuższy bok w terenie i na planie, by ustalić skalę podobieństwa: działki i planu (tzn. skalę mapy, bo nie pisze nic na ten temat).
2. Podzielić plan na dwa trójkąty o wspólnej podstawie, rysując jedną z przekątnych.
3. Narysować wysokości opuszczone na wspólną podstawę w każdym z trójkątów.
4. Zmierzyć podstawę i każdą wysokość z dokładnością do 1 mm.
5. Obliczyć pola każdego z trójkątów wg wzoru: P_Δ=1/2ah, gdzie a- to długość podstawy, zaś h – to długość wysokości.
6. Dodać pola dwóch trójkątów, by obliczyć pole działki na planie.
7. Powiększyć pola do rzeczywistych wartości (tu wykorzystać obliczoną skalę).
8. Sprawdzić, czy obliczone pole znacząco różni się od wyliczeń mierniczych (więcej, niż od 1 m²).

Podpisano:  Michał Kowalski.

• Podsumowania doświadczenia:
  
  Podsumowanie doświadczenia ma kluczowe znaczenie dla realizacji celów. Dlatego uważam za konieczne wykorzystanie w podsumowaniu następujących uwag i wskazań:

1. Instrukcję zaplanowano tak, by nie powiększać najpierw wymiarów liniowych, ale zmusić uczniów do podjęcia samodzielnej decyzji jak ustalić pole działki wykorzystując pole uzyskane z pomiarów na planie i skalę wyznaczoną w punkcie 1. zadania B (sprawdzić czy nie istnieje potrzeba omówienia jak to konkretnie zrobić). Istnieje spore prawdopodobieństwo, że niektórzy uczniowie powiększą pole tylko wykorzystując krotność skali. W samodzielnym odkryciu, że: Stosunek pól figur podobnych równy jest kwadratowi skali podobieństwa warto wykorzystać następujące możliwości, które okażą się dostępne:
   
   Możliwość poprawnego ustalenia pola przez uczniów – wówczas należy poprosić ich o wyjaśnienie dlaczego taki wynik otrzymali i doprowadzić do klaryfikacji tego uzasadnienia. Można też w tym celu zorganizować pracę w podgrupach; w każdej musi się znaleźć choć jeden uczeń, któremu udało się poprawnie określić pole i jego zadaniem będzie wyjaśnienie innym. Wspólna klaryfikacja nastąpić powinna dopiero po tym etapie.
   
   Spostrzeżenie, że otrzymany wynik bardzo różni się (około k - krotnie) od ustaleń mierniczych – doprowadzić wówczas do odkrycia dlaczego – tę część raczej prowadzi nauczyciel.
   
   Można wykorzystać do analizy w punkcie 2. przykład z klasycznym prostokątem tak, jak to np. zaproponowano w podręczniku: Matematyka 3. Podręcznik dla gimnazjum. Wydanie 2011. Praca zbiorowa pod redakcją M. Dobrowolskiej.
   
   
2. Niezwykle istotną częścią badań będzie dyskusja błędu pomiaru nawiązująca do problemu oszacowań. Załóżmy, że otrzymane pole jest nieznacznie mniejsze od otrzymanego przez mierniczych. Co okazałoby się, gdybyśmy przyjęli odczyt podstawy i obydwu wysokości o milimetr dłuższy (dlaczego taka możliwość?). Analogiczna analiza w przypadku otrzymania nieco większego wyniku z pomiarów. Należy także uwzględnić w dyskusji ocenę uczniów, którzy dokonali odmiennego wyboru przekątnej (podstawy trójkątów).
   
   
3. Można zaproponować uczniom, jako kontynuację badań, wymyślenie doświadczenia, w którym kształt czworokąta byłby zmienną niezależną, pole – zmienną zależną, a długości boków zmienną kontrolną. W szczególności problemem do obmyślenia byłoby zbudowanie (konstrukcyjnie) modelu czworokąta, który posłużyłby do badań.

• Propozycja dokumentacji przeprowadzenia doświadczenia przez uczniów:

1. Pomiary i obliczenia proponuję wpisać do tabeli pomiarowej np. wg wzoru przedstawionego poniżej:
   

   wymiary	boki czworokąta				przekątna (wspólna podstawa trójkątów)	wysokość h1	wysokość h2	P∆1	P∆2	Pd= P∆1+P∆2
   rzeczywiste (m)	20 m	18 m	16 m	14 m
   na planie (cm)
   skala podobieństwa					wzór na pole trójkąta		P∆ = ½ a · h

2. Dokumentacja powinna zawierać rysunek z wykreśloną przekątną i wysokościami, by można było zweryfikować poprawność i ocenić, czy staranność wykonania nie wpłynęła na wynik doświadczenia.
3. Można posłużyć się kartą pracy według wzoru Au – dla doświadczeń, które nie są grą.
4. Bezpośrednio w karcie zaplanować miejsca na obliczenia. 

---

Podstawa programowa

• Cele, które zostaną osiągnięte w wyniku przeprowadzenia doświadczenia przez nauczyciela i uczniów pod kierunkiem nauczyciela:

a) wymagania ogólne – cele

• II Wykorzystywanie i interpretowanie reprezentacji: uczeń używa prostych, dobrze znanych obiektów matematycznych, interpretuje pojęcia matematyczne i operuje obiektami matematycznymi.
• III Modelowanie matematyczne: uczeń dobiera model matematyczny do prostej sytuacji, buduje model matematyczny danej sytuacji.
• IV Użycie i tworzenie strategii: uczeń stosuje strategię jasno wynikającą z treści zadania, tworzy strategię rozwiązania problemu.
• V Rozumowanie i argumentacja: uczeń prowadzi proste rozumowania, podaje argumenty uzasadniające poprawność rozumowania.

b) wymagania szczegółowe - treści nauczania

• 10 Figury płaskie: 9) uczeń oblicza pola i obwody  trójkątów i czworokątów; 10) zamienia jednostki pola; 11) oblicza wymiary wielokąta powiększonego lub pomniejszonego w danej skali; 12) oblicza stosunek pól wielokątów podobnych;
• 1 Liczby wymierne dodatnie: 6) uczeń szacuje wartości wyrażeń arytmetycznych;

---

Materiały do pobrania

• pdf Pola figur podobnych - procedura 262 KB
• pdf Pola figur podobnych - karta pracy - wersja A 261 KB
• doc Pola figur podobnych - karta pracy - wersja A 526 KB

---

Słowniczek

EKSPERYMENT, prowadzony zgodnie z metodą naukową, rozumiany jest jako proces, w trakcie którego badacz, uczeń, wprowadza zaplanowaną zmianę jednego czynnika i bada, jakie ta zmiana przynosi rezultaty, uważając przy tym, by pozostałe czynniki pozostały niezmienne.

 

OBSERWACJA rozumiana jako zaplanowane gromadzenie faktów, bez wprowadzania jakichkolwiek ingerencji w badane zjawisko. W trakcie obserwacji nie występuje zmienna niezależna, ponieważ nie ingerujemy w badany proces.

 

Eksperyment i obserwacja są realizowane zgodnie z metodą naukową, a to oznacza:

Postawienie PYTANIA BADAWCZEGO - Pytanie może być zadane przez uczniów lub zaproponowane przez nauczyciela. Pozwala to ukierunkować myśli i skoncentrować się na badanym problemie, uświadamia, że badania naukowe są wynikiem zaplanowanego działania.Dobrze skonstruowane pytanie badawcze jest pytaniem otwartym - uczeń sam chce znaleźć na nie odpowiedź.

Kolejnym krokiem jest postawienie HIPOTEZY, czyli prawdopodobnej, przewidywanej i wymyślonej przez uczniów odpowiedź na pytanie badawcze. Pamiętajmy, że przed wykonaniem eksperymentu nie ma złych lub dobrych hipotez, każda, nawet najbardziej śmiała jest dopuszczalna.

Kolejny etap to określenie ZMIENNYCH:

• ZMIENNA NIEZALEŻNA czyli to, co zmieniamy.
• ZMIENNA ZALEŻNA czyli wielkość, którą będziemy mierzyć, obserwować.
• ZMIENNE KONTROLNE czyli wszystko to, co musi zostać niezmienne.

ZMIENNA ZALEŻNA to parametr mierzony podczas doświadczenia, zmieniający się w zależności od zmian ZMIENNEJ NIEZALEŻNEJ.

  

W doświadczeniu naukowym pojawiają się również PRÓBY KONTROLNE. Bez kontroli nie można jednoznacznie stwierdzić, czy wyniki doświadczenia są wiarygodne. Kontrola pozytywna to dodatkowa próba, którą przeprowadzamy identycznie, jak próbę badawczą, ale z użyciem takiego czynnika (jeśli jest znany), który na pewno wywołuje pożądany efekt. Z kolei kontrola negatywna to dodatkowa próba, ale bez użycia czynnika, o którym wiemy, że wywołuje badane zjawisko. Z założenia, wynikiem tej próby będzie brak zmiany mierzonego parametru. Nie w każdym układzie doświadczalnym da się zaplanować obie próby kontrolne.

  

Zajęcia z pytaniem problemowym zakładają dyskusję między uczniami na podstawie dodatkowych pytań lub przykładów dostarczonych przez nauczyciela. Zajęcia te kształcą umiejętność doboru i formułowania argumentów, słuchania osób o innym stanowisku oraz wyciągania wniosków. W wyniku dyskusji cenne byłoby wypracowanie stanowiska, by uczniowie przekonali się, że każda konstruktywna rozmowa powinna zakończyć się rzetelnym podsumowaniem.

 

Gry dydaktyczne wykorzystują czynnik zabawy, co wspomaga przyswajanie wiedzy przez uczniów. Gry rozwijają pomysłowość, aktywność, samodzielność, umiejętność pracy w grupie oraz uczą radzenia sobie z emocjami. Grając uczymy się przez działanie i przeżywanie. Sukcesem jest osiągnięcie celu, a nie wygrana z innymi, czy zajęcie pierwszego miejsca. Najważniejsza w grze jest dydaktyka. Wygrywać mają wszyscy.

---

Bibliografia

Proponuję, jako wystarczające źródło wiedzy - możliwe do wykorzystania przez uczniów i ewentualnie nauczyciela dowolny podręcznik matematyki do gimnazjum traktujący o podobieństwie figur np.:

1.  Matematyka 3. Podręcznik dla gimnazjum. Wydanie 2011. Praca zbiorowa pod redakcją M. Dobrowolskiej.

---