Wiadomości ogólne
- Czas trwania zajęć: 40 minut
- Kontekst w jakim wprowadzono doświadczenie:
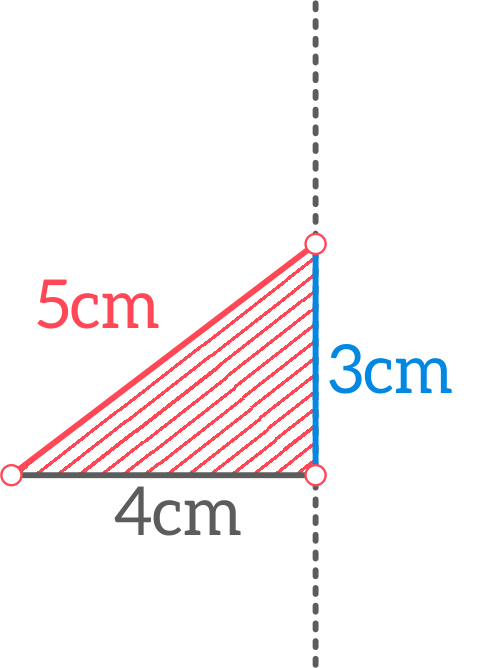
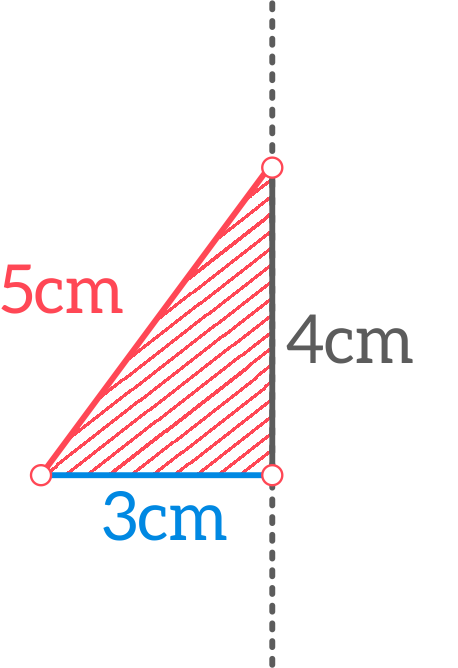
Trójkąt o bokach długości: 3cm, 4 cm, 5 cm obrócono o kąt 360o w przestrzeni trójwymiarowej względem osi zawierających poszczególne boki.
- Określenie wiedzy i umiejętności wymaganej u uczniów przed przystąpieniem do realizacji zajęć:
Uczeń wie jak powstają bryły obrotowe oraz zna sposób obliczania ich objętości. Ponadto uczeń potrafi rozpoznawać trójkąty prostokątne (tu trójkąt egipski) i obliczać pola trójkątów.
- Cele osiągnięte z wykorzystaniem doświadczenia:
Nauczyciela:
- kształcenie wyobraźni przestrzennej związanej z przekształceniem figury płaskiej na bryłę podczas obrotu,
- wykorzystanie wiadomości z planimetrii do ustalania parametrów pozwalających obliczyć objętość bryły złożonej ze stożków.
Uczniów:
- uczeń potrafi ustalić jaka bryła obrotowa powstanie podczas obrotu trójkąta względem wskazanej osi,
- uczeń potrafi obliczać objętość stożka.
- Pojęcia kluczowe:
- bryły obrotowe,
- stożek,
- promień podstawy,
- wysokość stożka,
- wysokość trójkąta,
- pole trójkąta,
- pole trójkąta prostokątnego,
- oś obrotu.
- Potencjalne pytania badawcze:
W którym przypadku otrzymano bryłę o największej objętości - wskaż właściwą twym zdaniem hipotezę:
- Gdy oś obrotu zawiera bok najkrótszy.
- Gdy oś obrotu zawiera bok średni.
- Gdy oś obrotu zawiera bok najdłuższy.
Doświadczenie
- Zmienne występujące w doświadczeniu:
- zmienna niezależna: bok, wokół którego obraca się trójkąt,
- zmienna zależna: objętość powstałej bryły,
- zmienna kontrolna: trójkąt, który się obraca.
Instrukcja wykonania doświadczenia:
- Naszkicuj każdą z trzech brył, które powstaną podczas obrotu trójkąta względem osi zawierających poszczególne boki.
Zobacz filmy "Jak powstaje stożek 1", "Jak powstaje stożek 2", "Jak powstaje stożek 3". Dokonaj ewentualnych korekt w swych szkicach.
- Ustal, jaka bryła powstanie w każdym z przypadków i dopasuj zaproponowane nazwy, wpisując je do tabeli doświadczenia.
- Ustal parametry: długość promienia podstawy i wysokości dla każdego z trzech przypadków i wpisz do tabeli doświadczenia. Możesz skorzystać ze wskazówki, gdybyś nie wiedziała/nie wiedział jak wyznaczyć promień dla bryły z trzeciego szkicu (odpowiednika filmu "Jak powstaje stożek 3") lub jak policzyć objętość powstałej bryły.
- Wykonaj obliczenia objętości (wpisz do tabeli) i na podstawie obliczeń zweryfikuj swoją hipotezę.
- Podsumowania doświadczenia:
Po zweryfikowaniu hipotezy należy przeprowadzić dyskusję wyników. Kluczowy problem (który proponuję najpierw omówić w parach) można sformułować następująco: „Który z parametrów bardziej wpływa na objętość stożka: promień, czy wysokość i dlaczego?”. Następnie, po odsłuchaniu ustaleń kilku par (przynajmniej jedna dobra odpowiedź w rozumieniu idei i poprawności argumentacji, ale niekoniecznie precyzji artykulacji), należy przeprowadzić dyskusję na forum klasy. Wniosek proponuję zapisać po poprawnym zredagowaniu.
- Propozycja dokumentacji przeprowadzenia doświadczenia przez uczniów:
Odpowiednik filmu "Jak powstaje stożek 1":
Odpowiednik filmu "Jak powstaje stożek 3":
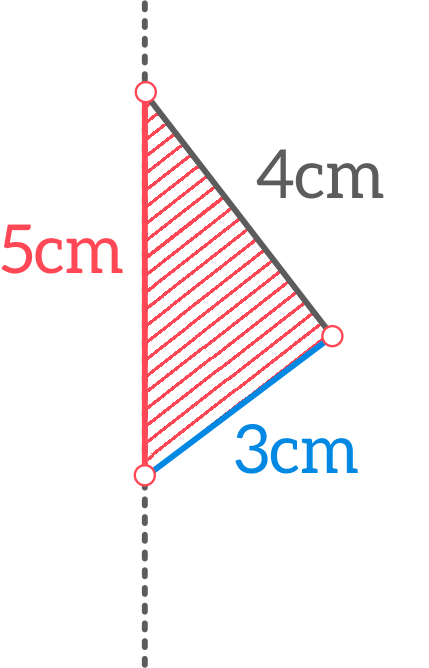
Tabela doświadczenia:
| Bryła ze szkicu |
Wybierz i wpisz nazwę: stożek o promieniu 3, stożek o wyskości 3 lub dwustożek |
Promień bryły | Wysokość bryły | Objętość bryły |
|
stożek 1 |
||||
|
stożek 2 |
||||
|
stożek 3 |
Na poniższym rysunku pokazano przekrój osiowy bryły powstałej z obrotu trójkąta wokół najdłuższego boku.
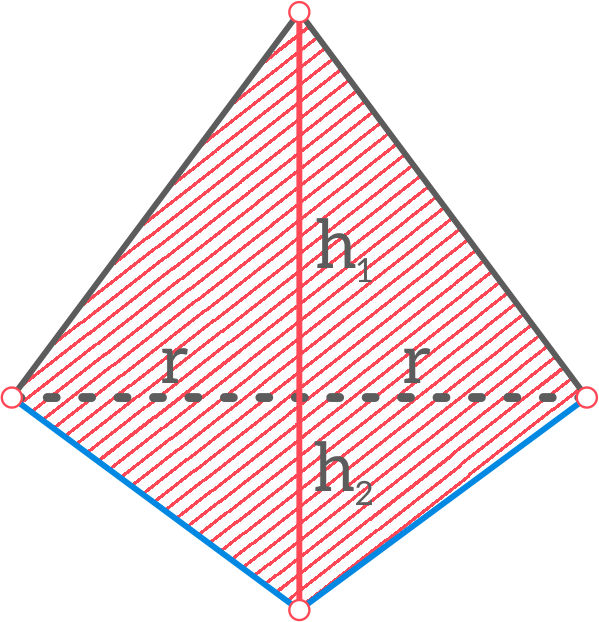
Ta bryła składa się z dwóch stożków „niebieskiego” i „szarego” (spójrz także na film „Jak powstaje stożek 3?”). Są one złączone podstawami więc obie mają ten sam promień r. Objętość „duostożka” jest sumą objętości stożka „szarego” i „niebieskiego”, więc można ją obliczyć wg wzoru:
Vd = Vb + Vn,
gdzie Vd - objętość „duostożka”, Vb - objętości stożka „szarego”, Vn - objętości stożka „niebieskiego”.
Vd=1/3πr2 · h1 + 1/3πr2 · h2 = 1/3πr2 · (h1 + h2)
Bez trudu zauważymy, że h1+h2 =5 cm. Pozostaje więc wyznaczyć wspólny dla obu stożków promień r. W tym celu wróćmy do analizy zależności w trójkącie, który obracając się tworzy „duostożek”. Pewnie z trójkątem o bokach 3, 4, 5 już spotkaliście się – to tzw. „trójkąt egipski” – jeden z pierwszych, znanych ludzkości trójkątów prostokątnych. Zauważmy, że promień r jest wysokością tego trójkąta odpowiadającą przeciwprostokątnej – jako podstawie. Inną parę: podstawa-wysokość tworzą przyprostokątne. Do wyznaczenia promienia wykorzystamy fakt, że pole prostokąta to stała – jej wartość nie zależy od wyboru pary podstawa-wysokość do obliczeń. Możemy zatem zapisać równanie (od razu wstawiono do niego liczby określające znane długości odcinków):
1/2 · 5 · r =1/2 · 3 · 4
5r=12
r=2 · 0,4
Obliczanie objętości poszczególnych brył:
Vs1=1/3π · ...2 · ...=
Vs2=1/3π · ...2 · ...=
Vs3=1/3π · ...2 · ...=
Podstawa programowa
- Cele, które zostaną osiągnięte w wyniku przeprowadzenia doświadczenia przez nauczyciela i uczniów pod kierunkiem nauczyciela:
a) wymagania ogólne – cele
- II Wykorzystywanie i interpretowanie reprezentacji: uczeń używa prostych, dobrze znanych obiektów matematycznych, interpretuje pojęcia matematyczne i operuje obiektami matematycznymi.
- III Modelowanie matematyczne: uczeń dobiera model matematyczny do prostej sytuacji, buduje model matematyczny danej sytuacji.
- IV Użycie i tworzenie strategii: uczeń stosuje strategię jasno wynikającą z treści zadania, tworzy strategię.
- V Rozumowanie i argumentacja: uczeń prowadzi proste rozumowania, podaje argumenty uzasadniające poprawność rozumowania.
b) wymagania szczegółowe - treści nauczania
- 11 Bryły: 2) uczeń oblicza pole powierzchni i objętość graniastosłupa prostego, ostrosłupa, walca, stożka, kuli (także w zadaniach osadzonych w kontekście praktycznym);
- 10 Figury płaskie: 9) uczeń oblicza pola i obwody trójkątów i czworokątów;
Materiały do pobrania
Słowniczek
EKSPERYMENT, prowadzony zgodnie z metodą naukową, rozumiany jest jako proces, w trakcie którego badacz, uczeń, wprowadza zaplanowaną zmianę jednego czynnika i bada, jakie ta zmiana przynosi rezultaty, uważając przy tym, by pozostałe czynniki pozostały niezmienne.
OBSERWACJA rozumiana jako zaplanowane gromadzenie faktów, bez wprowadzania jakichkolwiek ingerencji w badane zjawisko. W trakcie obserwacji nie występuje zmienna niezależna, ponieważ nie ingerujemy w badany proces.
Eksperyment i obserwacja są realizowane zgodnie z metodą naukową, a to oznacza:
Postawienie PYTANIA BADAWCZEGO - Pytanie może być zadane przez uczniów lub zaproponowane przez nauczyciela. Pozwala to ukierunkować myśli i skoncentrować się na badanym problemie, uświadamia, że badania naukowe są wynikiem zaplanowanego działania.Dobrze skonstruowane pytanie badawcze jest pytaniem otwartym - uczeń sam chce znaleźć na nie odpowiedź.
Kolejnym krokiem jest postawienie HIPOTEZY, czyli prawdopodobnej, przewidywanej i wymyślonej przez uczniów odpowiedź na pytanie badawcze. Pamiętajmy, że przed wykonaniem eksperymentu nie ma złych lub dobrych hipotez, każda, nawet najbardziej śmiała jest dopuszczalna.
Kolejny etap to określenie ZMIENNYCH:
- ZMIENNA NIEZALEŻNA czyli to, co zmieniamy.
- ZMIENNA ZALEŻNA czyli wielkość, którą będziemy mierzyć, obserwować.
- ZMIENNE KONTROLNE czyli wszystko to, co musi zostać niezmienne.
ZMIENNA ZALEŻNA to parametr mierzony podczas doświadczenia, zmieniający się w zależności od zmian ZMIENNEJ NIEZALEŻNEJ.
W doświadczeniu naukowym pojawiają się również PRÓBY KONTROLNE. Bez kontroli nie można jednoznacznie stwierdzić, czy wyniki doświadczenia są wiarygodne. Kontrola pozytywna to dodatkowa próba, którą przeprowadzamy identycznie, jak próbę badawczą, ale z użyciem takiego czynnika (jeśli jest znany), który na pewno wywołuje pożądany efekt. Z kolei kontrola negatywna to dodatkowa próba, ale bez użycia czynnika, o którym wiemy, że wywołuje badane zjawisko. Z założenia, wynikiem tej próby będzie brak zmiany mierzonego parametru. Nie w każdym układzie doświadczalnym da się zaplanować obie próby kontrolne.
Zajęcia z pytaniem problemowym zakładają dyskusję między uczniami na podstawie dodatkowych pytań lub przykładów dostarczonych przez nauczyciela. Zajęcia te kształcą umiejętność doboru i formułowania argumentów, słuchania osób o innym stanowisku oraz wyciągania wniosków. W wyniku dyskusji cenne byłoby wypracowanie stanowiska, by uczniowie przekonali się, że każda konstruktywna rozmowa powinna zakończyć się rzetelnym podsumowaniem.
Gry dydaktyczne wykorzystują czynnik zabawy, co wspomaga przyswajanie wiedzy przez uczniów. Gry rozwijają pomysłowość, aktywność, samodzielność, umiejętność pracy w grupie oraz uczą radzenia sobie z emocjami. Grając uczymy się przez działanie i przeżywanie. Sukcesem jest osiągnięcie celu, a nie wygrana z innymi, czy zajęcie pierwszego miejsca. Najważniejsza w grze jest dydaktyka. Wygrywać mają wszyscy.
Bibliografia
Proponuję, jako wystarczające źródło wiedzy - możliwe do wykorzystania przez uczniów, dowolny podręcznik matematyki do gimnazjum traktujący o objętościach i polach brył obrotowych np.:
1. Matematyka 3. Podręcznik dla gimnazjum. Wydanie 2011. Praca zbiorowa pod redakcją M. Dobrowolskiej.
2. Matematyka. Podręcznik z zadaniami. Gimnazjum klasa II. Małgorzata Świst, Barbara Zielińska. Oficyna Edukacyjna Krzysztof Pazdro Spółka z o.o., Warszawa 2009.