Wiadomości ogólne
- Czas trwania zajęć: ok. 40 minut
- Kontekst w jakim wprowadzono doświadczenie:
Proponuję wprowadzenie doświadczenia jako udział w scenariuszu zmagań rodzeństwa z praktycznym problemem przygotowania roztworu do peklowania szynki (pod nadzorem ich dziadka i z pomocą przyrządu, który nadzoruje poprawność obliczeń). Uczniowie czytają rozprawkę matematyczną i wykonują pojawiające się w niej polecenia.
- Określenie wiedzy i umiejętności wymaganej u uczniów przed przystąpieniem do realizacji zajęć:
Uczniowie potrafią wykonywać obliczenia procentowe i znają wzór na stężenie procentowe roztworów. Powinni także potrafić rozwiązywać równania zapisane w postaci proporcji.
- Cele osiągnięte z wykorzystaniem doświadczenia:
Nauczyciela:
- zrozumienie przez uczniów w jaki sposób można zmieniać stężenia roztworów,
- poprawne wykonywanie obliczeń procentowych z wykorzystaniem przekształcania wzoru na stężenie procentowe.
Uczniów:
- będziesz wiedział jak uzyskać roztwór o żądanym stężeniu,
- będziesz umiał obliczyć ile należy dodawać substancji rozpuszczanej, by korygować uzyskane stężenie.
- Pojęcia kluczowe:
- stężenie procentowe roztworów,
- substancja rozpuszczana,
- rozpuszczalnik,
- roztwór.
- Potencjalne pytania badawcze:
- Jak liczyć stężenia procentowe roztworów, by jajko nie okazało się mędrsze...?
- Hipoteza sformułowana przez uczniów:
- Hipoteza nie dotyczy pytania badawczego, gdyż to pytanie, dla doświadczenia typu zajęcia z pytaniem problemowym, dotyczy całego procesu badań i pełni także rolę pytania kluczowego.
- Uczniowie powinni zaproponować hipotezę dla punktu drugiego w zadaniu i nie chodzi tu o wartość bardzo dokładną, ale szacunkową. Dlatego uprawnione są zarówno szacunki na poziomie 0,01, jak i 0,1 kg.
Doświadczenie
- Zmienne występujące w doświadczeniu:
- zmienna niezależna: ilość substancji rozpuszczanej,
- zmienna zależna: stężenie roztworu,
- zmienna kontrolna: ilość rozpuszczalnika.
Instrukcja wykonania doświadczenia:
Zadanie A
Piotr i Ania szczególnie chętnie wybierali się w tym roku na święta. Dziadek dowiedział się bowiem, że w szkole nauczyli się przygotowywać roztwory o potrzebnym stężeniu i postanowił wtajemniczyć ich we własne arkana przygotowania roztworu do peklowania szynek. Szynki dziadka zawsze były dużo lepsze od kupowanych w sklepie, więc wnuczęta cieszyły się, że będą mogły poznać i kontynuować tę rodzinną tradycję.
Na wstępie dziadek wyjaśnił, że najważniejsze dla smaku szynki jest dobre przygotowanie roztworu do peklowania. On zawsze kupuje specjalny zestaw w sklepie, w którym zaopatrywał się jeszcze jego ojciec. Nie zna dokładnie zawartości tego zestawu, ale pewne jest, iż jednym z głównych składników jest po prostu sól kuchenna. Roztwór, który należy przyrządzić, musi być dokładnie 8-procentowy i aby być pewnym spełnienia tego istotnego wymogu, sprzedawca załącza do zestawu tajemnicze jajko, które „stoi na straży” poprawności uzyskania takiego stężenia. W instrukcji czytamy:
„Przygotuj odpowiedną ilość wody, by można było w niej całkowicie zanurzyć szynkę, zanurz jajko w wodzie, dosypuj bardzo powoli zestaw do rozpuszczania i mieszaj intensywnie, by całość rozpuszczała się nie opadając na dno garnka. W pewnym momencie jajko oderwie się od dna i wypłynie na powierzchnię, bacz by było jednak całkowicie zanurzone. Gdyby choć trochę jajka wystawało nad powierzchnię wody należy stopniowo dolać odrobinę wody, gdyż w innym wypadku stężenie byłoby za duże.”
- I do czego my Ci jesteśmy potrzebni Dziadku i nasze matematyczno-chemiczne umiejętności? – spytał Piotr. - Przecież ten przepis wyklucza potrzebę myślenia.
- Tu rzeczywiście niepotrzebna jest matematyka, ale muszę wam zdradzić, że czarodziejskie jajko dołączane jest do zestawu zaledwie od 10 lat i ja traktuję je raczej jako miły „gadżet”. Wciąż przygotowuję roztwór bardziej tradycyjnie. Najpierw sprawdzam ile wody zakryje szynkę. Później dolewam do pełnych litrów (czytaj kilogramów), by mi się lepiej liczyło stężenie. Następnie odważam potrzebną ilość zestawu do rozpuszczenia. I muszę przyznać, że jajko zostało naprawdę dobrze wykonane. Zawsze pływa tak jak pisze w instrukcji.
- To kto kogo pilnuje: jajko Ciebie Dziadku, czy Ty jajko?
- Wygląda na to, że mądrość jajka dorównuje mądrości kury – uśmiechnął się dziadek. - W każdym razie zobaczymy, czy nie okaże się mądrzejsze od Was.
W dobrym nastroju Piotr i Ania zabrali się do pracy. Z tęgimi minami czekali na ocenę jajka. Niestety musieli przeżyć rozczarowanie– jajko nie chciało wypływać na wierzch.
- Niemożliwe. To jajko jest jakieś głupie. Przecież do 3 litrów dodaliśmy dokładnie 3 x 8 dag soli.
Ania stanęła jednak w obronie mądrości jajka, proponując by obliczyć czy na pewno wyszło im dobre stężenie. Oboje pamiętali wzór na stężenie procentowe roztworów cp:
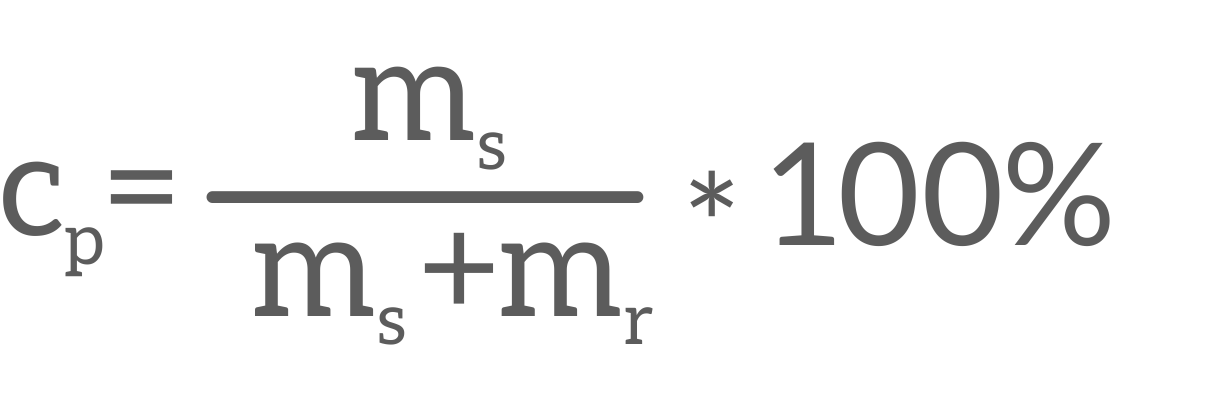
gdzie ms- to masa substancji rozpuszczanej podana w kilogramach, a mr – to masa rozpuszczalnika także wyrażona w kilogramach.
1. Wykonaj poniżej potrzebne obliczenia.
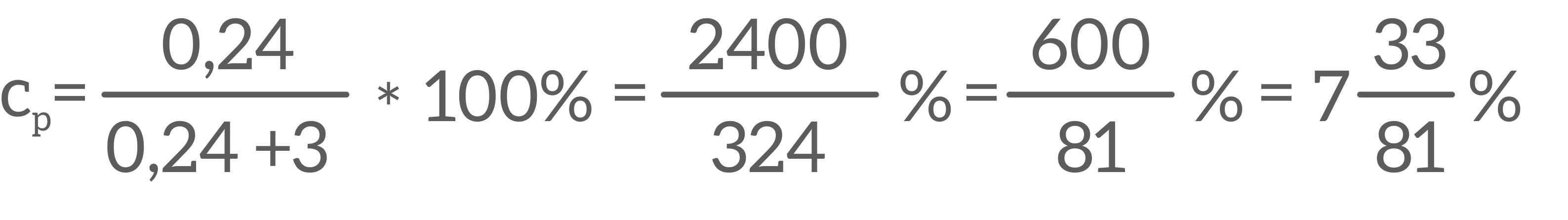
- Co teraz zrobić? - martwił się Piotr.
- Zawsze można skorzystać z instrukcji sklepowej – odrzekł dziadek.
- No ale to mało ambitne, może jednak obliczę ile soli trzeba dosypać – zaproponowała Ania.
- Dobrze, a ja już chyba zgadłem bez obliczeń - chwalił się Piotr.
- W razie czego mamy mądre jajko – śmiał się dziadek.
2. A czy wy umiecie przewidzieć (oszacować) ile substancji trzeba jeszcze dosypać?
Postawcie własną hipotezę. Następnie zapoznajcie się z obliczeniami Ani i przedyskutujcie w parach, czy jej rozumowanie jest poprawne:
„Mamy teraz 3,24 kg roztworu. Powinniśmy mieć 8% substancji rozpuszczanej czyli:
0,08·3,24kg=0,2592kg. Trzeba dosypać 1,92 dag".
(tu należy zrobić stopklatkę, by omówić wnioski par i ustalić czy rozumowanie Ani jest poprawne)
Dziadek stwierdził, że nie bardzo zna się na takiej matematyce. Zauważył, że nie ma także wystarczająco dokładnej wagi, więc zważy 2 dag, wrzuci jajko i będzie dosypywał powoli, by tej szczypty nie przesypać. Ale nawet po wrzuceniu całych 2 dag jajko nadal nie chciało wypłynąć.
- Chyba musimy zapisać jajko na korepetycje z matematyki – zaproponowała Ania.
- Ja bym nie przesądzał kogo – nieco zaczepnie odezwał się Piotr. - To w końcu ty zapomniałaś dosypać do mianownika.
- Co ty wygadujesz Piotrze, dosypuje się do roztworu? - żachnęła się Anna, ale natychmiast umilkła patrząc na wzór, gdyż zrozumiała swój błąd.
- To w które miejsce zabrnęliśmy? - spytał dziadek. - Zaraz to ustalimy Dziadku, tylko drobna poprawka w obliczeniach i będziemy wiedzieć jakie jest aktualne stężenie.
3. Wykonaj obliczenia pozwalające obliczyć aktualne stężenie roztworu.
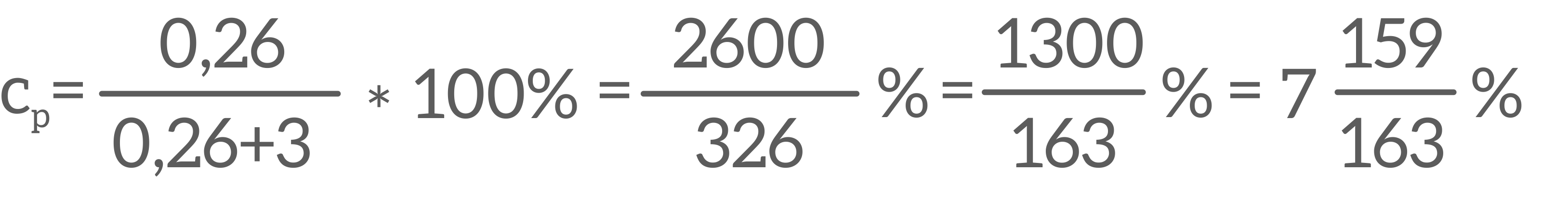
Dziadek zerknął na obliczenia swych wnucząt. Były identyczne.
- Naprawdę już odrobinę tylko brakuje - powiedział dziadek. - Tego nie da się nawet policzyć, bo trzeba dodawać do licznika i mianownika jednocześnie.
- Policzyć to by się dało, ale nie wiadomo, czy to da się zważyć na naszej wadze – rzekł Piotr. - Zresztą wiem już bez liczenia ile trzeba dodać.
- Jak zwykle się chwalisz – zaoponowała Ania.
- Tym razem wiem na pewno – trzeba dodać x.
Tym razem śmieli się wszyscy (może z wyjątkiem mądrali jajka). Aby poprawić sobie humor, zdecydowali także mimo wszystko policzyć tego iksa.
Jest tak: mamy 26 dag substancji rozpuszczonej w 300 dag wody. Po dodaniu x dag substancji musimy uzyskać stężenie 8%, czyli to, co rozpuszczamy powinno stanowić 0,08 = 2/25 całości. Matematycznie sprawa przedstawia się więc następująco:
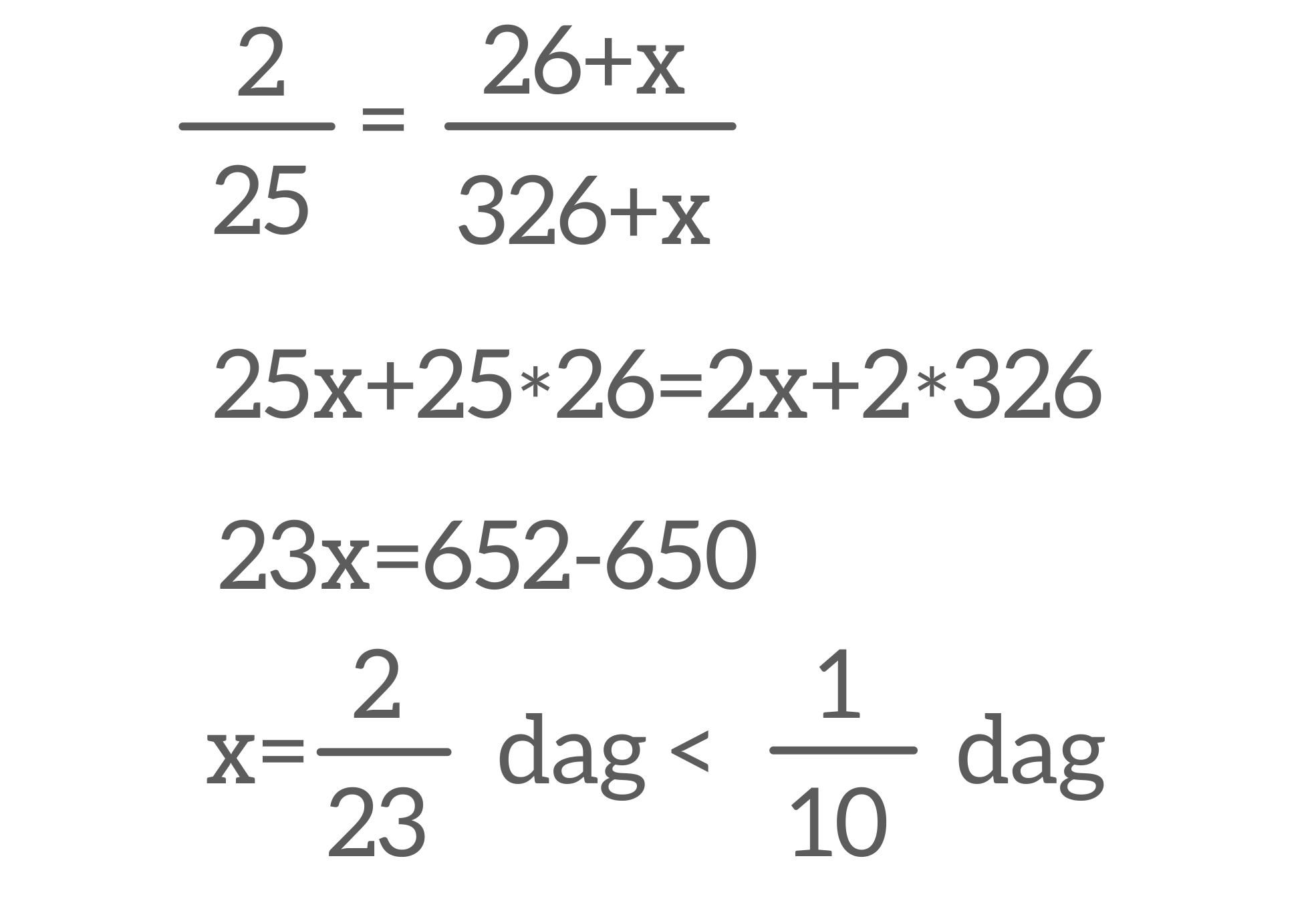
Jak widać pozostało do wsypania naprawdę odrobinę – mniej niż jeden gram.
4. W zespołach 4-osobowych spróbujcie sprawdzić, czy potraficie również poprawnie obliczyć wartość x.
Dziadek tymczasem powoli i bardzo ostrożnie wsypywał „iksa” do roztworu. Jajko niemal natychmiast majestatycznie wypłynęło na powierzchnię, ale wciąż jeszcze całe zanurzone.
Powoli zbliżały się święta.
- Podsumowania doświadczenia:
W zajęciach typu „z pytaniem problemowym” potrzebne były okresowe podsumowania kolejnych etapów procesu badawczego. Stanowią je:
- dyskusja w parach i jej podsumowanie na forum klasy dotycząca poprawności rozumowania Ani,
- podsumowania obliczeń prowadzonych indywidualnie i w zespołach 4-osobowych poprzez informację zwrotną dostępną w formie linków do poprawnych obliczeń.
Ponadto na zakończenie warto podsumować kluczowe doświadczenie, które powinno stać się udziałem uczniów. Może to być np. ocena prawdziwości zdań:
- Dodając 10 dag soli do 1 kg wody, otrzymamy solankę 10-cio procentową PRAWDA/FAŁSZ
- Jeśli w 4 kg roztworu jest 1 kg soli, to stężenie wynosi 20% PRAWDA/FAŁSZ
- Dodając 1 kg soli do 4 kg wody, otrzymamy stężenie 25% PRAWDA/FAŁSZ
- Propozycja dokumentacji przeprowadzenia doświadczenia przez uczniów:
Dokumentację doświadczenia powinny stanowić:
- Zapis hipotezy – odpowiedzi na pytanie badawcze w 2. punkcie zadania.
- Obliczenia dotyczące instrukcji 1., 2. i 4. punktu zadania.
- Określenie zmiennych - poprawnie podano w "Zmiennych występujących w doświadczeniu".
Uwaga: W materiałach do pobrania załączono materiał dodatkowy w formie komiksu dla ucznia, który uzupełnia zakres przedstawiony powyżej.
Podstawa programowa
- Cele, które zostaną osiągnięte w wyniku przeprowadzenia doświadczenia przez nauczyciela i uczniów pod kierunkiem nauczyciela:
a) wymagania ogólne – cele
- II Wykorzystywanie i interpretowanie reprezentacji: uczeń używa prostych, dobrze znanych obiektów matematycznych, interpretuje pojęcia matematyczne i operuje obiektami matematycznymi.
- III Modelowanie matematyczne: uczeń dobiera model matematyczny do prostej sytuacji, buduje model matematyczny danej sytuacji.
- IV Użycie i tworzenie strategii: uczeń stosuje strategię jasno wynikającą z treści zadania, tworzy strategię rozwiązania problemu.
- V Rozumowanie i argumentacja: uczeń prowadzi proste rozumowania, podaje argumenty uzasadniające poprawność rozumowania.
b) wymagania szczegółowe - treści nauczania
- 5 Procenty: 1) uczeń przedstawia część pewnej wielkości jako procent lub promil tej wielkości i odwrotnie; 2) oblicza procent danej liczby; 3) oblicza liczbę na podstawie danego jej procentu; 4) stosuje obliczenia procentowe do rozwiązywania problemów w kontekście praktycznym, np. oblicza ceny po podwyżce lub obniżce o dany procent, wykonuje obliczenia związane z VAT, oblicza odsetki dla lokaty rocznej.
Materiały do pobrania
Słowniczek
EKSPERYMENT, prowadzony zgodnie z metodą naukową, rozumiany jest jako proces, w trakcie którego badacz, uczeń, wprowadza zaplanowaną zmianę jednego czynnika i bada, jakie ta zmiana przynosi rezultaty, uważając przy tym, by pozostałe czynniki pozostały niezmienne.
OBSERWACJA rozumiana jako zaplanowane gromadzenie faktów, bez wprowadzania jakichkolwiek ingerencji w badane zjawisko. W trakcie obserwacji nie występuje zmienna niezależna, ponieważ nie ingerujemy w badany proces.
Eksperyment i obserwacja są realizowane zgodnie z metodą naukową, a to oznacza:
Postawienie PYTANIA BADAWCZEGO - Pytanie może być zadane przez uczniów lub zaproponowane przez nauczyciela. Pozwala to ukierunkować myśli i skoncentrować się na badanym problemie, uświadamia, że badania naukowe są wynikiem zaplanowanego działania.Dobrze skonstruowane pytanie badawcze jest pytaniem otwartym - uczeń sam chce znaleźć na nie odpowiedź.
Kolejnym krokiem jest postawienie HIPOTEZY, czyli prawdopodobnej, przewidywanej i wymyślonej przez uczniów odpowiedź na pytanie badawcze. Pamiętajmy, że przed wykonaniem eksperymentu nie ma złych lub dobrych hipotez, każda, nawet najbardziej śmiała jest dopuszczalna.
Kolejny etap to określenie ZMIENNYCH:
- ZMIENNA NIEZALEŻNA czyli to, co zmieniamy.
- ZMIENNA ZALEŻNA czyli wielkość, którą będziemy mierzyć, obserwować.
- ZMIENNE KONTROLNE czyli wszystko to, co musi zostać niezmienne.
ZMIENNA ZALEŻNA to parametr mierzony podczas doświadczenia, zmieniający się w zależności od zmian ZMIENNEJ NIEZALEŻNEJ.
W doświadczeniu naukowym pojawiają się również PRÓBY KONTROLNE. Bez kontroli nie można jednoznacznie stwierdzić, czy wyniki doświadczenia są wiarygodne. Kontrola pozytywna to dodatkowa próba, którą przeprowadzamy identycznie, jak próbę badawczą, ale z użyciem takiego czynnika (jeśli jest znany), który na pewno wywołuje pożądany efekt. Z kolei kontrola negatywna to dodatkowa próba, ale bez użycia czynnika, o którym wiemy, że wywołuje badane zjawisko. Z założenia, wynikiem tej próby będzie brak zmiany mierzonego parametru. Nie w każdym układzie doświadczalnym da się zaplanować obie próby kontrolne.
Zajęcia z pytaniem problemowym zakładają dyskusję między uczniami na podstawie dodatkowych pytań lub przykładów dostarczonych przez nauczyciela. Zajęcia te kształcą umiejętność doboru i formułowania argumentów, słuchania osób o innym stanowisku oraz wyciągania wniosków. W wyniku dyskusji cenne byłoby wypracowanie stanowiska, by uczniowie przekonali się, że każda konstruktywna rozmowa powinna zakończyć się rzetelnym podsumowaniem.
Gry dydaktyczne wykorzystują czynnik zabawy, co wspomaga przyswajanie wiedzy przez uczniów. Gry rozwijają pomysłowość, aktywność, samodzielność, umiejętność pracy w grupie oraz uczą radzenia sobie z emocjami. Grając uczymy się przez działanie i przeżywanie. Sukcesem jest osiągnięcie celu, a nie wygrana z innymi, czy zajęcie pierwszego miejsca. Najważniejsza w grze jest dydaktyka. Wygrywać mają wszyscy.
Bibliografia
1. Procenty: Matematyka 1. Podręcznik dla gimnazjum. Wydanie 2009. Praca zbiorowa pod redakcją M. Dobrowolskiej,
2. Zadania dotyczące stężeń procentowych: Matematyka 2. Podręcznik dla gimnazjum. Wydanie 2010. Praca zbiorowa pod redakcją M. Dobrowolskiej,
3. Artykuł Artura Krila pt. ”Średnie i dźwignie”, Matematyka w szkole nr 67 listopad/grudzień 2012.