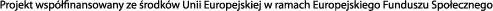Wiadomości ogólne
- Czas trwania zajęć: 40 minut
- Kontekst w jakim wprowadzono doświadczenie:
Dwie trzyosobowe grupy badaczy określały średnie zarobki w przedsiębiorstwie dystrybucji energii elektrycznej „Amper Bold”. Oto relacja z ich badań:
Zespół Adama: analizował dane o zarobkach poszczególnych pracowników z rozbiciem na działy, w których pracowali.
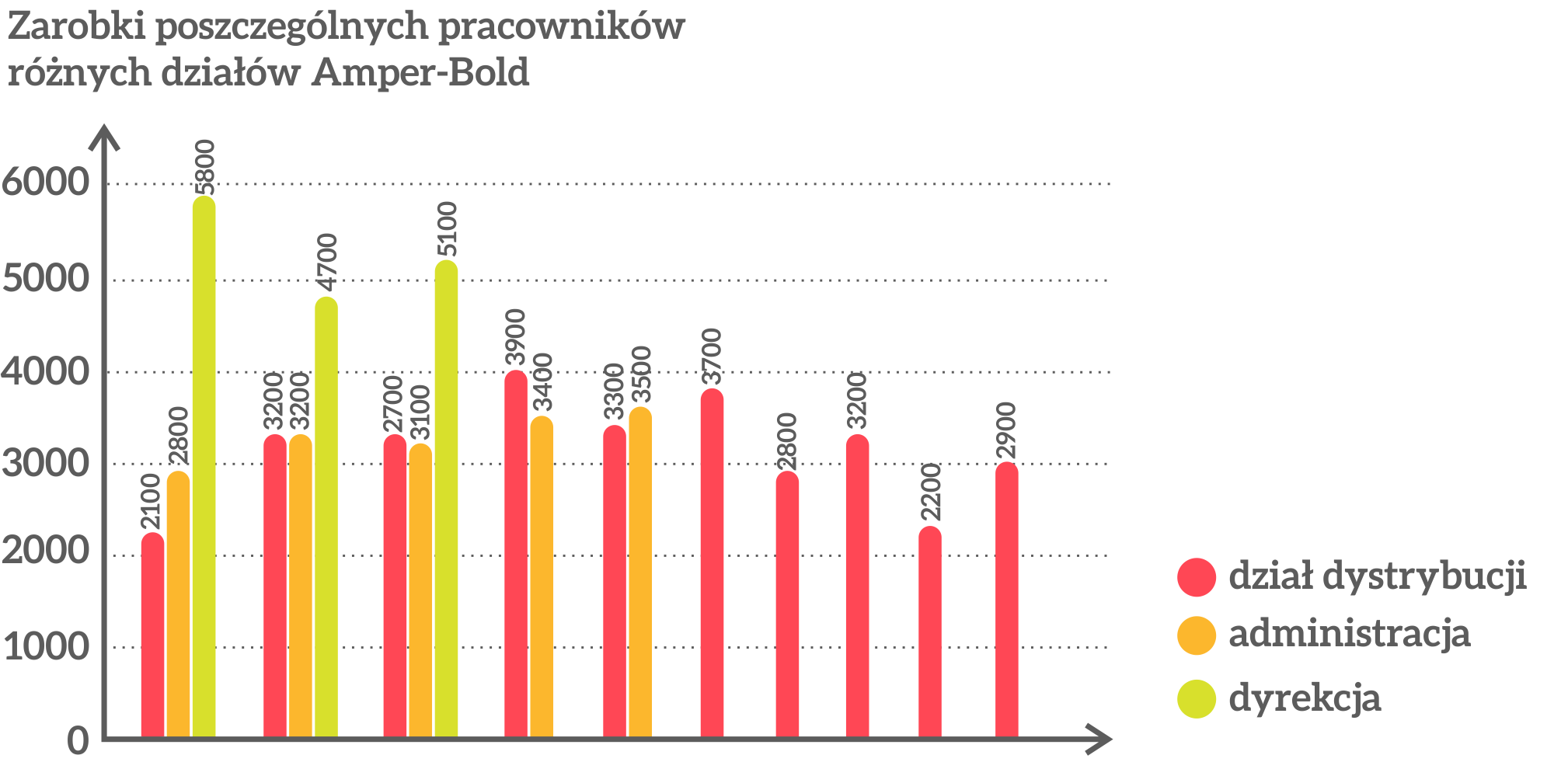
Obliczenie średniego zarobku w firmie: (3000+3200+5200):3=3800
Zespół Oli: analizował dane o zarobkach tych samych pracowników zebrane w tabeli – osobno mężczyźni, a osobno kobiety:
| zarobki | średnia | ||||||||||
| kobiety | 5100 | 3700 | 3200 | 4700 | 3200 | 3200 | 3400 | 3100 | 3700 | ||
| mężczyźni | 2100 | 2700 | 3900 | 3300 | 2800 | 220 | 2900 | 2800 | 3500 | 5800 | 3002 |
| Średni zarobek firmy | 3351 | ||||||||||
- Określenie wiedzy i umiejętności wymaganej u uczniów przed przystąpieniem do realizacji zajęć:
Umiejętność obliczania średniej arytmetycznej.
- Cele osiągnięte z wykorzystaniem doświadczenia:
Nauczyciela:
- odkrycie metodologii obliczania średniej arytmetycznej dla zbiorów różnolicznych,
- samodzielne ustalenie warunku, przy którym średnia średnich jest średnią.
Uczniów:
- uczeń będzie rozumiał dlaczego średnia ze średnich zazwyczaj nie jest średnią.
- Pojęcia kluczowe:
- średnia arytmetyczna.
- Potencjalne pytania badawcze:
Oceń, która hipoteza jest prawdziwa:
- Poprawnie średnie zarobki firmy ustalił zespół Adama.
- Poprawnie średnie zarobki firmy ustalił zespół Oli.
- Żaden z zespołów nie określił poprawnie średnich zarobków firmy.
Doświadczenie
- Zmienne występujące w doświadczeniu:
- zmienna niezależna: liczebność podzbiorów, dla których obliczano średnie cząstkowe,
- zmienna zależna: średnia obliczona jako średnia ze średnich,
- zmienna kontrolna: zbiór płac wszystkich pracowników firmy.
Uwaga! Wprawdzie zmieniała się także ilość podzbiorów wykorzystywanych do obliczania średniej w oparciu o złą metodologię, ale kluczowe znaczenie dla otrzymania złego wyniku ma „nierównoliczność podzbiorów”, a nie ich ilość.
Instrukcja wykonania doświadczenia:
- Zbierz w jedną tabelę dane o zarobkach pracowników firmy (bez rozbicia na kategorie - czyli nie tak, jak to uczyniły zespoły badawcze Adama bądź Oli).
- Oblicz średnią arytmetyczną dla tego zbioru.
- Porównaj z wynikami poszczególnych zespołów badawczych i zweryfikuj swoją hipotezę.
- Podsumowania doświadczenia:
Postawcie hipotezę, który z dwóch poniżej wskazanych czynników miał decydujący wpływ na otrzymanie niepoprawnych wyników przez zespoły badawcze:
- podział danych na podzbiory,
- nierównoliczność tych podzbiorów.
Zaplanujcie doświadczenie, za pomocą którego da się sprawdzić, która z hipotez jest prawdziwa (praca w zespołach 4-osobowych). Przedyskutujcie swoje projekty i napiszcie instrukcję doświadczenia. Uzgodnijcie ostateczną treść instrukcji.
- Propozycja dokumentacji przeprowadzenia doświadczenia przez uczniów:
Dane potrzebne do obliczenia średniej można zebrać w tabeli. Można także skopiować dane z tabeli Oli do utworzonej elektronicznie w arkuszu kalkulacyjnym i wykorzystać funkcję obliczania średniej. Poniżej proponowany wzór:
| nr pracownika |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | średni zarobek |
| zarobek |
Podstawa programowa
- Cele, które zostaną osiągnięte w wyniku przeprowadzenia doświadczenia przez nauczyciela i uczniów pod kierunkiem nauczyciela:
a) wymagania ogólne – cele
- II Wykorzystywanie i interpretowanie reprezentacji: uczeń używa prostych, dobrze znanych obiektów matematycznych, interpretuje pojęcia matematyczne i operuje obiektami matematycznymi.
- III Modelowanie matematyczne: uczeń dobiera model matematyczny do prostej sytuacji, buduje model matematyczny danej sytuacji.
- IV Użycie i tworzenie strategii: uczeń stosuje strategię jasno wynikającą z treści zadania, tworzy strategię rozwiązania problemu.
- V Rozumowanie i argumentacja: uczeń prowadzi proste rozumowania, podaje argumenty uzasadniające poprawność rozumowania.
b) wymagania szczegółowe - treści nauczania
- Statystyka opisowa i wprowadzenie do rachunku prawdopodobieństwa: 1) uczeń interpretuje dane przedstawione za pomocą tabel, diagramów słupkowych i kołowych, wykresów; 2) wyszukuje, selekcjonuje i porządkuje informacje z dostępnych źródeł; 3) przedstawia dane w tabeli, za pomocą diagramu słupkowego lub kołowego; 4) wyznacza średnią arytmetyczną i medianę zestawu danych;
Materiały do pobrania
Słowniczek
EKSPERYMENT, prowadzony zgodnie z metodą naukową, rozumiany jest jako proces, w trakcie którego badacz, uczeń, wprowadza zaplanowaną zmianę jednego czynnika i bada, jakie ta zmiana przynosi rezultaty, uważając przy tym, by pozostałe czynniki pozostały niezmienne.
OBSERWACJA rozumiana jako zaplanowane gromadzenie faktów, bez wprowadzania jakichkolwiek ingerencji w badane zjawisko. W trakcie obserwacji nie występuje zmienna niezależna, ponieważ nie ingerujemy w badany proces.
Eksperyment i obserwacja są realizowane zgodnie z metodą naukową, a to oznacza:
Postawienie PYTANIA BADAWCZEGO - Pytanie może być zadane przez uczniów lub zaproponowane przez nauczyciela. Pozwala to ukierunkować myśli i skoncentrować się na badanym problemie, uświadamia, że badania naukowe są wynikiem zaplanowanego działania.Dobrze skonstruowane pytanie badawcze jest pytaniem otwartym - uczeń sam chce znaleźć na nie odpowiedź.
Kolejnym krokiem jest postawienie HIPOTEZY, czyli prawdopodobnej, przewidywanej i wymyślonej przez uczniów odpowiedź na pytanie badawcze. Pamiętajmy, że przed wykonaniem eksperymentu nie ma złych lub dobrych hipotez, każda, nawet najbardziej śmiała jest dopuszczalna.
Kolejny etap to określenie ZMIENNYCH:
- ZMIENNA NIEZALEŻNA czyli to, co zmieniamy.
- ZMIENNA ZALEŻNA czyli wielkość, którą będziemy mierzyć, obserwować.
- ZMIENNE KONTROLNE czyli wszystko to, co musi zostać niezmienne.
ZMIENNA ZALEŻNA to parametr mierzony podczas doświadczenia, zmieniający się w zależności od zmian ZMIENNEJ NIEZALEŻNEJ.
W doświadczeniu naukowym pojawiają się również PRÓBY KONTROLNE. Bez kontroli nie można jednoznacznie stwierdzić, czy wyniki doświadczenia są wiarygodne. Kontrola pozytywna to dodatkowa próba, którą przeprowadzamy identycznie, jak próbę badawczą, ale z użyciem takiego czynnika (jeśli jest znany), który na pewno wywołuje pożądany efekt. Z kolei kontrola negatywna to dodatkowa próba, ale bez użycia czynnika, o którym wiemy, że wywołuje badane zjawisko. Z założenia, wynikiem tej próby będzie brak zmiany mierzonego parametru. Nie w każdym układzie doświadczalnym da się zaplanować obie próby kontrolne.
Zajęcia z pytaniem problemowym zakładają dyskusję między uczniami na podstawie dodatkowych pytań lub przykładów dostarczonych przez nauczyciela. Zajęcia te kształcą umiejętność doboru i formułowania argumentów, słuchania osób o innym stanowisku oraz wyciągania wniosków. W wyniku dyskusji cenne byłoby wypracowanie stanowiska, by uczniowie przekonali się, że każda konstruktywna rozmowa powinna zakończyć się rzetelnym podsumowaniem.
Gry dydaktyczne wykorzystują czynnik zabawy, co wspomaga przyswajanie wiedzy przez uczniów. Gry rozwijają pomysłowość, aktywność, samodzielność, umiejętność pracy w grupie oraz uczą radzenia sobie z emocjami. Grając uczymy się przez działanie i przeżywanie. Sukcesem jest osiągnięcie celu, a nie wygrana z innymi, czy zajęcie pierwszego miejsca. Najważniejsza w grze jest dydaktyka. Wygrywać mają wszyscy.
Bibliografia
1. Matematyka 2. Podręcznik dla gimnazjum. Wydanie 2010. Praca zbiorowa pod redakcją M. Dobrowolskiej.
2. Matematyka Europejczyka. Podręcznik dla gimnazjum. Klasa 2 Ewa Madziąg, Małgorzata Muchowska. Wydawnictwo Helion – rok wydania: 2013.
3. Matematyka 2001. Podręcznik do gimnazjum 2. Anna Bazyluk, Anna Dubiecka, Barbara Dubiecka-Kruk, Zbigniew Góralewicz, Tomasz Malicki, Piotr Piskorski, Henryk Sienkiewicz, Andrzej Ziemieńczuk.